题目内容
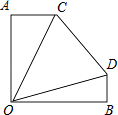
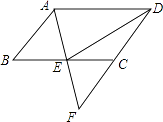
【题目】发现与探究:如图,△ABC和△DCE中,AC=BC,DC=EC,∠ACB=∠DCE=45°,点B,C,E三点共线,且BC:CE=2:1,连接AE,BD. 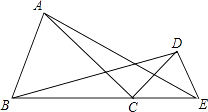
(1)在不添加辅助线和字母的情况下,请在图中找出一对全等三角形(用“≌”表示),并加以证明;
(2)求tan∠BDC的值.
【答案】
(1)解:△BCD≌△ACE,
∵∠ACB=∠DCE,
∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,
在△BCD与△ACE中 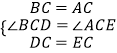 ,
,
∴△BCD≌△ACE(SAS)
(2)解:作AF⊥BE,如图:
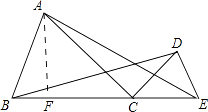
∵BC:CE=2:1,
∴设BC=2k,CE=k,
在Rt△AFC中,AC=BC=2k,∠ACF=45°,
∴FC=ACcos45°=2k× ![]() ,EF=FC+CE=
,EF=FC+CE= ![]() k+k=(
k+k=( ![]() +1)k,
+1)k,
∵∠FAC=45°,
∴AF= ![]() k,
k,
由(1)得△BCD≌△ACE,
∴∠BDC=∠AEC,
∴在Rt△AFE中,tan∠BDC=tan∠AEC= ![]()
【解析】(1)根据SAS证明△BCD与△ACE全等即可;(2)作AF⊥BE,利用三角函数进行解答即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目