Question

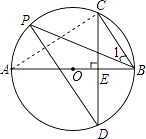
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1=∠C．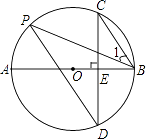
（1）求证：CB∥PD；
（2）若BC=6，sin∠P= ，求AB的值．

Answer 1

【答案】
（1）证明：∵∠1=∠C，∠C=∠P，

∴∠1=∠P，

∴CB∥PD．

（2）解：连接AC，

∵AB是⊙O的直径，

∴∠ACB=90°．

∵CD⊥AB，

∴ = ，

∴∠P=∠CAB，

∴sin∠CAB= = ．

∵BC=6，

∴AB=15．

【解析】（1）根据∠1=∠C及圆周角定理可得出∠1=∠P，由此可得出结论；（2）连接AC，根据圆周角定理得出∠ACB=90°，再由垂径定理得出 = ，故可得出∠P=∠CAB，根据锐角三角函数的定义即可得出结论．
【考点精析】利用垂径定理和圆周角定理对题目进行判断即可得到答案，需要熟知垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．