题目内容
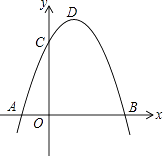
【题目】如图,一条抛物线y=﹣x(x﹣2)(0≤x≤2)的一部分,记为C1 , 它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2 , 交x轴于点A2 , ;将C2绕点A2旋转180°得到C3 , 交x轴于A3;…如此进行下去,直至得到C6 , 若点P(2017,y)在抛物线Cn上,则y= . 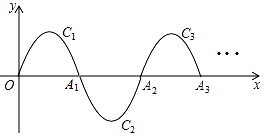
【答案】2
【解析】解:∵一段抛物线C1:y=﹣x(x﹣2)(0≤x≤2), ∴图象C1与x轴交点坐标为:(0,0),(2,0),
∵将C1绕点A1旋转180°得C2 , 交x轴于点A2;,
∴抛物线C2:y=(x﹣2)(x﹣4)(2≤x≤4),
将C2绕点A2旋转180°得C3 , 交x轴于点A3;
…
∴P(2017,y)在抛物线C1009上,
∵n=1009是奇数,
∴P(2017,y)在x轴的上方,y=2,
∴当x=2017时,y=2.
所以答案是2.
【考点精析】认真审题,首先需要了解二次函数图象的平移(平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减),还要掌握抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.)的相关知识才是答题的关键.

练习册系列答案
相关题目