题目内容
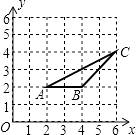
【题目】如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y= ![]() (x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( )
(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为( ) 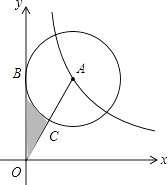
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]()
C.2 ![]()
D.2 ![]()
【答案】D
【解析】解:连接AB,BC, ∵点A在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴S△AOB= ![]() ×4
×4 ![]() =2
=2 ![]() ,
,
∴ ![]() OBAB=2
OBAB=2 ![]() ,
,
∵点C为OA中点,
∴BC= ![]() OA=AC,
OA=AC,
∴△ABC是等边三角形,
∴∠OAB=60°,
∴ ![]() =tan60°=
=tan60°= ![]() ,
,
∴OB= ![]() AB,
AB,
∴ ![]()
![]() ABAB=2
ABAB=2 ![]() ,
,
∴AB=2,
∴S扇形= ![]() =
= ![]() =
= ![]() ,
,
∴S阴影=S△AOB﹣S扇形=2 ![]() ﹣
﹣ ![]() ,
,
故选D.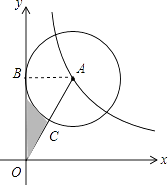
【考点精析】关于本题考查的比例系数k的几何意义和扇形面积计算公式,需要了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能得出正确答案.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?