Question

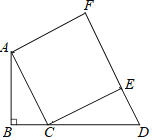
【题目】如图，四边形ACEF为正方形，以AC为斜边作Rt△ABC，∠B=90°，AB=4，BC=2，延长BC至点D，使CD=5，连接DE．

（1）求正方形的边长；

（2）求DE的长．

Answer 1

【答案】（1）正方形边长为2；（2）DE=

【解析】

(1)根据题意△ABC为直角三角形，AB=4，BC=2，则可以根据勾股定理求出AC的长，即正方形的边长；

(2)通过证明△ABC与△CED相似，利用相似三角形的性质即可求得答案.

(1)在Rt△ABC中，AB=4，BC=2，

AC===2，

∴正方形边长为2；

(2)∵∠B=90°，

∴∠BAC+∠BCA=90°，

∵∠ACE=90°，

∴∠BCA+∠ECD=90°，

∴∠BAC=∠ECD，

又∵=，

∴△ABC∽△CED，

∴=，

∴DE=．