题目内容
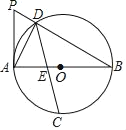
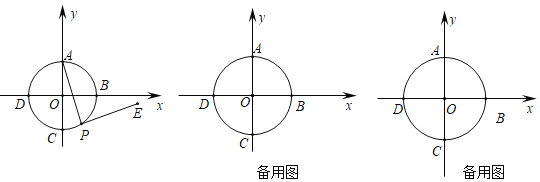
【题目】如图,半径为4且以坐标原点为圆心的圆O交x轴,y轴于点B、D、A、C,过圆上的动点![]() 不与A重合
不与A重合![]() 作
作![]() ,且
,且![]() 在AP右侧
在AP右侧![]() .
.
![]() 当P与C重合时,求出E点坐标;
当P与C重合时,求出E点坐标;
![]() 连接PC,当
连接PC,当![]() 时,求点P的坐标;
时,求点P的坐标;
![]() 连接OE,直接写出线段OE的取值范围.
连接OE,直接写出线段OE的取值范围.
【答案】(1)(8,-4);(2) 点P的坐标为![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
![]() 当P与C重合时,因为
当P与C重合时,因为![]() ,
,![]() 的半径为4,且
的半径为4,且![]() 在AP右侧
在AP右侧![]() ,所以
,所以![]() ,所以E点坐标为
,所以E点坐标为![]() ;
;
![]() 作
作![]() 于点F,证明
于点F,证明![]() ∽
∽![]() ,可求得CF长,在
,可求得CF长,在![]() 中求得PF的长,进而得出点P的坐标;
中求得PF的长,进而得出点P的坐标;
![]() 连结OP,OE,AB,BE,AE,证明
连结OP,OE,AB,BE,AE,证明![]() ∽
∽![]() ,可得
,可得![]() ,根据
,根据![]() ,即可得出OE的取值范围.
,即可得出OE的取值范围.
解:![]() 当P与C重合时,
当P与C重合时,
![]() ,
,![]() 的半径为4,且
的半径为4,且![]() 在AP右侧
在AP右侧![]() ,
,
![]() ,
,
![]() 点坐标为
点坐标为![]() ;
;
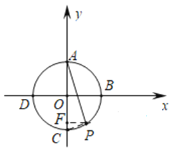
![]() 如图,作
如图,作![]() 于点F,
于点F,
![]() 为
为![]() 的直径,
的直径,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点P的坐标为
点P的坐标为![]() 或
或![]() ;
;
![]() 如图,连结OP,OE,AB,BE,AE,
如图,连结OP,OE,AB,BE,AE,

![]() ,
,![]() 都为等腰直角三角形,
都为等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目