��Ŀ����
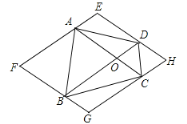
����Ŀ����ABC�ǵȱ������Σ���D������BC�ϵ�һ������(��D�����B��C�غ�)����ADE����ADΪ�ߵĵȱ������Σ�����E��BC��ƽ���ߣ�������AC�ڵ�G������BE��
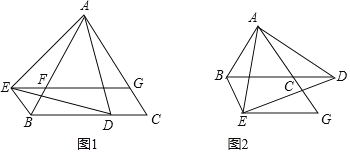
��1����ͼ1��ʾ������D���߶�BC��ʱ����֤���ı���BCGE��ƽ���ı��Σ�
��2����ͼ2��ʾ������D��BC���ӳ�����ʱ����1���еĽ����Ƿ����������˵�����ɣ�
��3������D�˶���ʲôλ��ʱ���ı���BCGE�����Σ���˵�����ɣ�
���𰸡���1��֤������������2�������Գ��������ɼ���������3������D��BC���ӳ����ϣ�CD=BCʱ���ı���BCGE�����Σ����ɼ�������
��������
��1������SAS����֤����AEB�ա�ADC������ȫ�������ε����ʵõ���ABE=��ACB=60�����õ�BE��CG������ƽ���ı��ε��ж�����֤�����ۣ�
��2�����գ�1����֤���������
��3���ֵ�D��BC�ϡ���D��BC���ӳ���������������������ε��ж��������
��1��֤�����ߡ�ABC�ǵȱ������Σ�
��AB=AC����ABC=��ACB=��BAC=60����
�ߡ�ADE�ǵȱ������Σ�
��AE=AD����EAD=60����
���EAB=��DAC��
����AEB����ADC��
��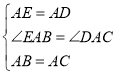 ��
��
���AEB�ա�ADC(SAS)��
���ABE=��ACB=60������EBC+��ACB=��ABE+��ABC+��ACB=180����
��BE��CG��
��EG��BC��
���ı���BCGE��ƽ���ı��Σ�
��2���⣺��1���еĽ����Գ�����
�������£��ɣ�1����֪����ABE�ա�ACD��
���BEA=��CDA��
��EG��BC��
���G=��ACB=60������GED=��BDE�����BEG+��G=��BEA+��AED+��GED+��G=��AED+(��CDA+��BDE)+��G=180������BE��CG��
�֡�EG��BC��
���ı���BCGE��ƽ���ı��Σ�
��3���⣺����D��BC��ʱ���ɣ�2����֪����ABE�ա�ACD��
��BE=CD��
��BE=CD��BC�����ı���BCGE�������Σ�
����D��BC���ӳ����ϣ�CD=BCʱ���ı���BCGE�����Σ�
�ɣ�2����֪����ABE�ա�ACD���ı���BCGE��ƽ���ı��Σ�
��BE=CD=BCʱ���ı���BCGE�����Σ�