题目内容
【题目】如图,任意四边形ABCD,对角线AC、BD交于O点,过各顶点分别作对角线AC、BD的平行线,四条平行线围成一个四边形EFGH.试想当四边形ABCD的形状发生改变时,四边形EFGH的形状会有哪些变化?完成以下题目:
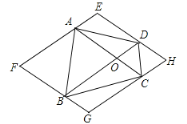
(1)①当ABCD为任意四边形时,四边形EFGH为___________;
②当四边形ABCD为矩形时,四边形EFGH为___________;
③当四边形ABCD为菱形时,四边形EFGH为___________;
④当四边形ABCD为正方形时,四边形EFGH为___________;
(2)请对(1)中①③你所写的结论进行证明
【答案】(1)①平行四边形;②菱形;③矩形;④正方形;(2)证明见解析
【解析】
(1)①根据平行于同一条直线的两直线平行可得EF∥BD∥GH,EH∥AC∥FG,然后根据平行四边形的定义即可求出结论;
②根据平行四边形的性质可得EH=AC,EF=BD,然后根据矩形的性质可得AC=BD,然后根据菱形的定义即可求出结论;
③根据菱形的性质可得AC⊥BD,从而证出EF⊥EH,然后根据矩形的定义即可求出结论;
④根据平行四边形的性质和正方形的性质可得:EH=AC,EF=BD,AC=BD,AC⊥BD,从而得出EH=EF,EF⊥EH,然后根据正方形的定义即可得出结论;
(2)根据平行于同一条直线的两直线平行可得EF∥BD∥GH,EH∥AC∥FG,然后根据平行四边形的定义即可证出①;根据菱形的性质可得AC⊥BD,从而证出EF⊥EH,然后根据矩形的定义即可证出③.
解:(1)①由题意可知:EF∥BD,GH∥BD,EH∥AC,FG∥AC
∴EF∥BD∥GH,EH∥AC∥FG
∴四边形EFGH、四边形EACH和四边形EFBD都为平行四边形
故答案为:平行四边形;
②由①知四边形EFGH、四边形EACH和四边形EFBD都为平行四边形
∴EH=AC,EF=BD
∵四边形ABCD为矩形
∴AC=BD
∴EH=EF
∴四边形EFGH为菱形
故答案为:菱形;
③∵四边形ABCD为菱形
∴AC⊥BD
∵EF∥BD,EH∥AC,
∴EF⊥EH
∵四边形EFGH为平行四边形
∴四边形EFGH为矩形
故答案为:矩形;
④由①知四边形EFGH为平行四边形,EF∥BD,EH∥AC,四边形ABCD为正方形
∴EH=AC,EF=BD,AC=BD,AC⊥BD
∴EH=EF,EF⊥EH
∴四边形EFGH为正方形
故答案为:正方形;
(2)①证明如下:
由题意可知:EF∥BD,GH∥BD,EH∥AC,FG∥AC
∴EF∥BD∥GH,EH∥AC∥FG
∴四边形EFGH为平行四边形;
③证明如下:
∵四边形ABCD为菱形
∴AC⊥BD
∵EF∥BD,EH∥AC,
∴EF⊥EH
∵四边形EFGH为平行四边形
∴四边形EFGH为矩形

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案