题目内容
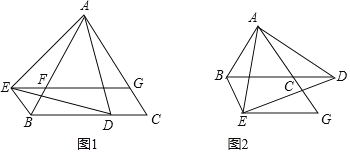
【题目】已知，如图．AD∥BE，∠1＝∠2，求证：∠A＝∠E．请完成解答过程．
证明：∵AD∥BE（已知）
∴∠A＝∠ （ ）
又∵∠1＝∠2（已知）
∴AC∥ （ ）
∴∠3＝∠ （两直线平行，内错角相等）
∴∠A＝∠E（等量代换）
【答案】3，两直线平行，同位角相等，DE，内错角相等，两直线平行，E．
【解析】
根据平行线的性质与判定即可求解.
证明：∵AD∥BE（已知），
∴∠A＝∠3（两直线平行，同位角相等），
又∵∠1＝∠2（已知），
∴AC∥DE（内错角相等，两直线平行），
∴∠3＝∠E（两直线平行，内错角相等），
∴∠A＝∠E（等量代换），
故答案为：3，两直线平行，同位角相等，DE，内错角相等，两直线平行，E．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共
个，小李做摸球实验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，如表是实验中的一组统计数据：
摸球的次数 |
|
|
|
|
|
|
|
摸到白球的次数 |
|
|
|
|
|
|
|
摸到白球的频率 |
|
|
|
|
|
|
|
请估计：当实验次数为
次时，摸到白球的频率将会接近________；（精确到
）
假如你摸一次，你摸到白球的概率
（摸到白球）
________；
如何通过增加或减少这个不透明盒子内球的具体数量，使得在这个盒子里每次摸到白球的概率为
？
