题目内容
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
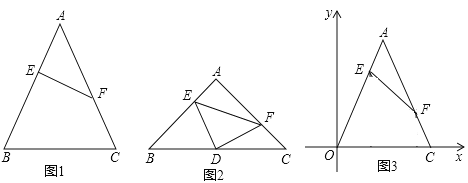
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
【答案】
(1)
证明:∵∠DAB=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∴∠D+∠ACD=180°﹣30°=150°,
∵∠BCD=∠ACD+∠ACB=150°,
∴∠D=∠ACB,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=ABAD,
∴四边形ABCD为“可分四边形”
(2)
解:∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵AC2=ABAD,
∴AD:AC=AC:AB,
∴△ADC∽△ACB,
∴∠D=∠ACB,
∵∠DCB=∠DAB,
∴∠DCB=∠DCA+∠ACB=2∠DAC,
∵∠DAC+∠D+∠ACB=180°,
∴∠DAC+2∠DAC=180°,
解得:∠DAC=60°,
∴∠DAB=120°
(3)8
【解析】(3)∵四边形ABCD为“可分四边形”,AC=4,
∴ABAD=AC2=16,
当DA⊥DB时,△DAB的最大,最大面积为8,
故答案为:8.
(1)由已知得出∠DAC=∠CAB=30°,由三角形内角和定理得出∠D+∠ACD=150°,由∠BCD=∠ACD+∠ACB=150°,得出∠D=∠ACB,证明△ADC∽△ACB.得出对应边成比例,得出AC2=ABAD,即可得出结论;(2)由已知条件可证得△ADC∽△ACB,得出D=∠ACB,再由已知条件和三角形内角和定理得出∠DAC+2∠DAC=180°,求出∠DA=60°,即可得出∠DAB的度数;(3)根据“可分四边形”的定义求出ABAD,计算即可.

 名校课堂系列答案
名校课堂系列答案