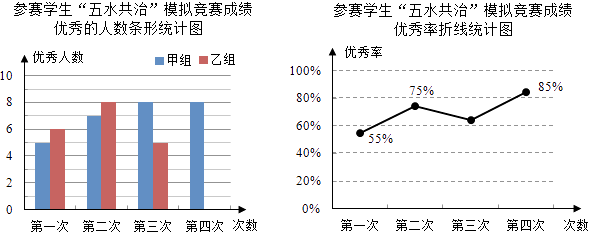
题目内容
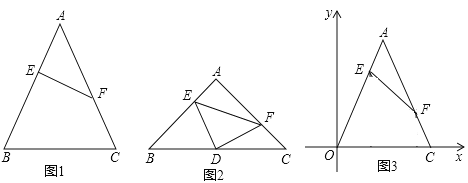
【题目】定义:如图1,等腰△ABC中,点E,F分别在腰AB,AC上,连结EF,若AE=CF,则称EF为该等腰三角形的逆等线.
(1)如图1,EF是等腰△ABC的逆等线,若EF⊥AB,AB=AC=5,AE =2,求逆等线EF的长;
(2)如图2,若等腰直角△DEF的直角顶点D恰好为等腰直角△ABC底边BC上的中点,且点E,F分别在AB,AC上,求证:EF为等腰△ABC的逆等线;
(3)如图3,边长为6的等边三角形△AOC的边OC与X轴重合,EF是该等边三角形的逆等线.F点的坐标为(5,![]() );试求点E的坐标(若需要,本题可以直接应用结论:在直角三角形中,30°角所对的直角边等于斜边的一半.)
);试求点E的坐标(若需要,本题可以直接应用结论:在直角三角形中,30°角所对的直角边等于斜边的一半.)
【答案】(1)![]() (2)见解析 (3)E(2,
(2)见解析 (3)E(2,![]() )
)
【解析】
(1)由逆等线的性质可求得CF和AE,由条件可求得AF,在Rt△AEF中,由勾股定理可求得EF的长;
(2)连接AD,可证明△EDA≌△FDC,可求得AE=CF,可证得结论;
(3)过E、F分别作EG⊥OC于G , FH⊥OC于H,由勾股定理可得FC![]() ,由逆等线知AE=2,在△OEG中,分别求得OG、EG即可得点E的坐标.
,由逆等线知AE=2,在△OEG中,分别求得OG、EG即可得点E的坐标.
解:
(1)∵EF是等腰△ABC的逆等线,
∴CF=AE=2,又AB=AC=5,
∴AF=3,
∵EF⊥AB,
∴EF=![]() =
=![]() ,
,
(2)连结AD,在等腰Rt△ABC中,点D为底边上中点,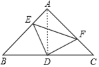
∴AD=CD且∠ADC=90°,
又∵DE=DF且∠EDF=90°,
∴∠EDA=90°-∠ADF=∠FDC,
在△EDA和△FDC中,
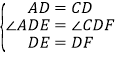 ,
,
∴△EDA≌△FDC(SAS),
∴AE=CF,
∴EF为等腰△ABC的逆等线;
(3)过E、F分别作EG⊥OC于G , FH⊥OC于H,
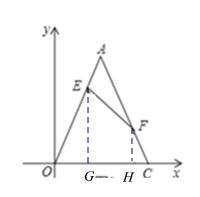
∵F点的坐标为(5,![]() ),
),
∴FH=![]() ,OH=5,
,OH=5,
则HC=OC-OH=6-5=1,
在Rt△FHC中,FC=![]() ,
,
∴AE=FC=2,
∴OE=OA-AE=6-2=4,
又∵FH⊥OC,∠AOC=60°,
∴∠OEG=30°,
∴OG=![]() OE=2,( 在直角三角形中,30°角所对的直角边等于斜边的一半)
OE=2,( 在直角三角形中,30°角所对的直角边等于斜边的一半)
∴EG=![]() =
=![]() =
=![]() ,
,
∴E(2,![]() ).
).