题目内容
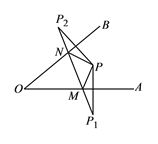
【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
【答案】15 96°
【解析】
P点关于OA的对称是点P1,P点关于OB的对称点P2,故有PM=P1M,PN=P2N.由此即可得到△PMN的周长.根据四边形内角和为360°,可得出∠P1PP2的度数,根据等腰三角形的性质和三角形外角的性质可得出∠PNM+∠PMN的度数,再根据三角形内角和定理即可得出∠MPN的度数.
∵P点关于OA的对称是点P1,P点关于OB的对称点P2,∴PM=P1M,PN=P2N,PP2⊥OB,PP1⊥OA,∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15,∠P1PP2=360°-90°-90°-42°=138°,∠P2=∠NPP2,∠P1=∠P1PM,∴∠PNM=2∠P2,∠PMN=2∠P1,∴∠PNM+∠PMN=2∠P1+2∠P2=2(180°-∠P1PP2)=84°,∴∠MPN=180°-(∠PNM+∠PMN)=180°-84°=96°.
故答案为:15,96°.

练习册系列答案
相关题目