Question

【题目】在四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，DF平分∠CDA．

（1）作出符合本题的几何图形；

（2）求证：BE∥DF．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

（1）根据题意画出图形即可；
（2）根据四边形内角和为360°可得∠ADC+∠ABC=180°，然后再根据角平分线定义可得∠ADF=∠FDE=∠ADC，∠EBF=∠EBC=∠ABC，再证明∠DFA=∠EBF可得结论．

（1）如图所示：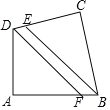

（2）证明：∵四边形ABCD中，∠A=∠C=90°，
∴∠ADC+∠ABC=180°，
∵BE平分∠ABC，DF平分∠CDA，
∴∠ADF=∠FDE=∠ADC，∠EBF=∠EBC=∠ABC，
∴∠FBE+∠FDE=90°，
∵∠A=90°，
∴∠AFD+∠ADF=90°，
∴∠AFD+∠EDF=90°，
∴∠DFA=∠EBF，
∴DF∥EB．