��Ŀ����
����Ŀ���Ķ����ϣ���ͼ��1������������Aʾ����Ϊa��B���ʾ����Ϊb�����A����B�ľ����ΪAB���߶�AB�ij��������ұߵ�����ȥ��ߵ�����ʾ����AB��b��a��
![]()
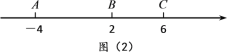
������⣺��ͼ��2���������ϵ�A��ʾ�����ǣ�4����B��ʾ������2����C��ʾ������6��
��1������������һ��D����AD��3�����D��ʾ������
��2����A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�3����λ���ȵ��ٶ������˶�������t���ӹ�������A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC�����A��ʾ�������ú�t�Ĵ���ʽ��ʾ����BC���ڶ��٣��ú�t�Ĵ���ʽ��ʾ����
��3�����ʣ�3BC��AB��ֵ�Ƿ�����ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
���𰸡���1����7��1�� ��2����4��t t��4 ��3�����䣬���ɼ�����.
��������
��1����D��ʾ����Ϊa���ɾ���ֵ���������ó������
��2���ֱ��ʾ��t���A��B��C�ֱ��Ӧ����������AC���ɣ�
��3����ʾ��BC��AB����������ɵó����ۣ�
��1����D��ʾ����Ϊa��
��AD=3��
��|-4-a|=3��
��ã�a=-7��-1��
��2������A�����ƶ�t����λ���ȣ����ƶ���ĵ��ʾ����Ϊ-4-t��
����B�͵�C�ֱ������˶�2t��3t����λ���ȣ����ƶ���ĵ��ʾ�����ֱ�Ϊ2+2t��6+3t����BC=��6+3t��-��2+2t��=t+4��
��3��AB=��2+2t��-��-4-t��=3t+6��
3BC��AB=3��t+4��-��3t+6��=6��
��3BC��AB��ֵ����ʱ��t�ı仯���ı�.