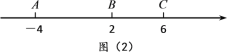题目内容
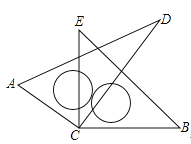
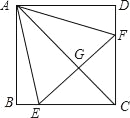
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.
A. 5 B. 4 C. 3 D. 2
【答案】C
【解析】
试题∵四边形ABCD是正方形,
∴AB=AD,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∴①说法正确;
∵BC=DC,
∴BC-BE=CD-DF,
∴CE=CF,
∴△ECF是等腰直角三角形,
∴∠CFE=45°
∴∠AFD=75°
∴∠DAF=15°
∴②正确;
∵AC是正方形ABCD的对角线,∴∠BCA=45°
∴AC⊥EF
又CE=CF
∴AC垂直平分EF,
∴③正确;
在AD上取一点G,连接FG,使AG=GF,

则∠DAF=∠GFA=15°,
∴∠DGF=2∠DAF=30°,
设DF=1,则AG=GF=2,DG=![]() ,
,
∴AD=CD=2+![]() ,CF=CE=CD-DF=1+
,CF=CE=CD-DF=1+![]() ,
,
∴EF=![]() CF=
CF=![]() +
+![]() ,而BE+DF=2,
,而BE+DF=2,
∴④说法错误;
∵S△ABE+S△ADF=2S△ABE=2×![]() AD×DF=2+
AD×DF=2+![]() ,
,
S△CEF=![]() CE×CF=
CE×CF=![]() ,
,
∴⑤正确
故选B.
考点: 1.正方形的性质;2.全等三角形的判定与性质;3.等边三角形的性质.

 名校名卷单元同步训练测试题系列答案
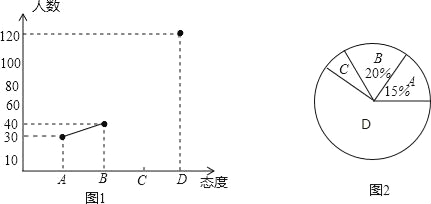
名校名卷单元同步训练测试题系列答案【题目】中学生带手机上学的现象越来越受到社会的关注,为此某记者随机调查了市区某校七年级若干名中学生家长对这种现象的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).统计员在将测试数据绘制成图表时发现,反对漏统计6人,赞成漏统计4人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题:
家长对中学生带手机上学各项态度人数统计表和统计图:
态度 | 调整前人数 | 调整后人数 |
A.无所谓 | 30 | 30 |
B.基本赞成 | 40 | 40 |
C.赞成 | ||
D.反对 | 114 | 120 |
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)填写统计表,并根据调整后数据补全折线统计图;
(3)根据抽样调查结果,请你估计该市城区6000名中学生家长中有多少名家长持反对态度?