题目内容
【题目】在矩形ABCD中,∠ABC的平分线交AD于点E,∠BED的平分线交DC于点F,若AB=6,点F恰为DC的中点,则BC=(结果保留根号)
【答案】3+3 ![]()
【解析】解:延长EF和BC,交于点G,如图所示: ∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=6,
∴等腰直角△ABE中,BE= ![]() =6
=6 ![]() ,
,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE=6 ![]() ,
,
∵∠G=∠DEF,∠EFD=∠GFC,
∴△EFD∽△GFC
∴ ![]() =1,
=1,
∴CG=DE,
设CG=DE=x,则AD=6+x=BC,
∵BG=BC+CG,
∴6 ![]() =6+x+x,
=6+x+x,
解得:x=3 ![]() ﹣3
﹣3
∴BC=6+(3 ![]() ﹣3)=3+3
﹣3)=3+3 ![]() ;
;
故答案为:3+3 ![]() .
.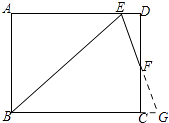
先延长EF和BC,交于点G,再根据条件可以判断三角形ABE为等腰直角三角形,并求得其斜边BE的长,然后根据条件判断三角形BEG为等腰三角形,最后根据△EFD∽△GFC得出CG与DE的相等关系,并根据BG=BC+CG进行计算即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)
|
| ||||||||||||||||||||||||||||||
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?







