题目内容
下列因式分解中,正确的有( )
①4a﹣a3b2=a(4﹣a2b2);
②x2y﹣2xy+xy=xy(x﹣2);
③﹣a+ab﹣ac=﹣a(a﹣b﹣c);
④9abc﹣6a2b=3abc(3﹣2a);
⑤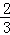 x2y+
x2y+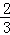 xy2=
xy2=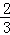 xy(x+y)
xy(x+y)
①4a﹣a3b2=a(4﹣a2b2);
②x2y﹣2xy+xy=xy(x﹣2);
③﹣a+ab﹣ac=﹣a(a﹣b﹣c);
④9abc﹣6a2b=3abc(3﹣2a);
⑤
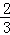 x2y+
x2y+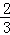 xy2=
xy2=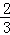 xy(x+y)
xy(x+y)| A.0个 | B.1个 | C.2个 | D.5个 |
B
试题分析:根据因式分解的定义对各选项分析判断后利用排除法求解.
解:在①中,还能继续运用平方差公式,最后结果为:a(2+ab)(2﹣ab);
在②中,显然漏了一项,最后结果应为xy(x﹣3);
在③中,注意各项符号的变化,最后结果应为:﹣a(1﹣b+c);
在④中,显然两项的公因式应为:3ab;
在⑤中,正确运用了提公因式法.故正确的有一个.
故选B.
点评:注意在运用提公因式法的时候,不要出现类似②、③、④的错误,特别注意符号的变化和不要漏项.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目