题目内容
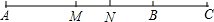 如图,点C是线段AB延长线上的一点,使AC=4BC,M、N分别是线段AB、AC的中点.若MN=3cm,则线段AC的长为
如图,点C是线段AB延长线上的一点,使AC=4BC,M、N分别是线段AB、AC的中点.若MN=3cm,则线段AC的长为24
24
cm.分析:设BC=acm,则AC=4acm,求出AB=3acm,求出BM=
acm,NC=2acm,代入MN=3cm=MB+BC-NC,得出方程
a+a-2a=3,求出方程的解即可.
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:设BC=acm,则AC=4acm,
则AB=4acm-acm=3acm,
∵M、N分别是线段AB、AC的中点,
∴BM=
AB=
acm,NC=
AC=2acm,
∵MN=3cm=MB+BC-NC,
∴
a+a-2a=3,
a=6,
∴AC=4a=24(cm).
故答案为:24.
则AB=4acm-acm=3acm,
∵M、N分别是线段AB、AC的中点,
∴BM=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∵MN=3cm=MB+BC-NC,
∴
| 3 |
| 2 |
a=6,
∴AC=4a=24(cm).
故答案为:24.
点评:本题考查了两点间的距离,关键是得出关于a的方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,点C是线段AB的中点,点D是线段BC的中点,下面等式不正确的是( )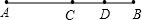
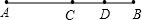
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
 10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )
10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )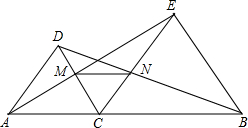 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( ) 如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )
如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )