题目内容
 10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )
10、如图,点D是线段AB与线段BC的垂直平分线的交点,∠B=40°,则∠ADC等于( )分析:连接BD、AC.设∠1=x.根据线段垂直平分线的性质,得AD=BD,BD=CD.根据等边对等角,得∠1=∠2=x,∠4=∠ABD=40°+x.根据三角形的内角和定理,得∠ADB=180°-2∠4=100°-2x,∠BDC=180°-2x,进而求得∠ADC.
解答: 解:连接BD,AC.设∠1=x,
解:连接BD,AC.设∠1=x,
∵点D是线段AB与线段BC的垂直平分线的交点,
∴AD=BD,BD=CD,
∴∠1=∠2=x,∠4=∠ABD=40°+x,
根据三角形的内角和定理,得∠ADB=180°-2∠4=100°-2x,∠BDC=180°-2x,
∴∠ADC=∠BDC-∠ADB=80°.
故选D.
 解:连接BD,AC.设∠1=x,
解:连接BD,AC.设∠1=x,∵点D是线段AB与线段BC的垂直平分线的交点,
∴AD=BD,BD=CD,
∴∠1=∠2=x,∠4=∠ABD=40°+x,
根据三角形的内角和定理,得∠ADB=180°-2∠4=100°-2x,∠BDC=180°-2x,
∴∠ADC=∠BDC-∠ADB=80°.
故选D.
点评:此题综合考查了线段垂直平分线的性质、等边对等角的性质以及三角形的内角和定理;作出辅助线是正确解答本题的关键.

练习册系列答案
相关题目
如图,点C是线段AB的中点,点D是线段BC的中点,下面等式不正确的是( )
| A、CD=AD-BC | ||
| B、CD=AC-DB | ||
C、CD=
| ||
D、CD=
|
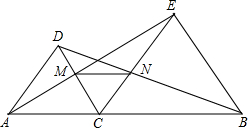 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N. 如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( ) 如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )
如图,点C是线段AB的中点,点D是线段BC的中点,则下列结论中错误的是( )