题目内容
已知:如图,点C是线段AB上的任意一点(点C与A、B点不重合),分别以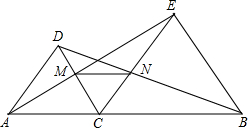 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
(1)求证:△ACE≌△DCB;
(2)如果AB的长为10cm,MN=ycm,AC=xcm.
①请写出y与x之间的函数关系式,并指出自变量的取值范围.
②当点C在何处时MN的长度最长?并求MN的最大长度.
 AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.
AC、BC为边在直线AB的同侧作等边△ACD和等边△BCE,AE与CD相交于点M,BD和CE相交于点N.(1)求证:△ACE≌△DCB;
(2)如果AB的长为10cm,MN=ycm,AC=xcm.
①请写出y与x之间的函数关系式,并指出自变量的取值范围.
②当点C在何处时MN的长度最长?并求MN的最大长度.
分析:(1)先根据△ACD和△BCE是等边三角形可得出AC=CD,BC=CE,∠ACD=∠BCE=60°,故可得出∠ACD+∠DCE=∠BCE+∠DCE,∠DCB=∠ACE,由SAS定理即可得出结论;
(2)①由(1)中的结论得出△ACM≌△DCN,即CM=CN,△MCN是等边三角形可得出MN∥AB,可先假设其存在,设AC=x,MN=y,进而由平行线分线段成比例即可得出结论;
②由①中y与x的函数关系式可直接得出结论.
(2)①由(1)中的结论得出△ACM≌△DCN,即CM=CN,△MCN是等边三角形可得出MN∥AB,可先假设其存在,设AC=x,MN=y,进而由平行线分线段成比例即可得出结论;
②由①中y与x的函数关系式可直接得出结论.
解答:(1)证明:∵△ACD和△BCE是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,∠DCB=∠ACE,
在△ACE与△DCB中,
∵
,
∴△ACE≌△DCB;
(2)①∵△ACE≌△DCB,
∴∠CAE=∠BDC,
∴△ACM≌△DCN,
∴CM=CN,
又∵∠MCN=180°-60°-60°=60°,
∴△MCN是等边三角形,
∴∠MNC=∠NCB=60°,
∴MN∥AB.
∴
=
,
∵AB的长为10cm,MN=ycm,AC=xcm.
∴
=
,即y=-
x2+x(0<x<10);
②∵由①可知,y=-
x2+x(0<x<10),即y=-
(x-5)2+2.5;
∴当x=5时,MN的值最大,MN的最大长度为2.5cm,即当C点是AB中点时,线段MN的最大长度是2.5cm.
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,∠DCB=∠ACE,
在△ACE与△DCB中,
∵
|
∴△ACE≌△DCB;
(2)①∵△ACE≌△DCB,
∴∠CAE=∠BDC,
∴△ACM≌△DCN,
∴CM=CN,
又∵∠MCN=180°-60°-60°=60°,
∴△MCN是等边三角形,
∴∠MNC=∠NCB=60°,
∴MN∥AB.
∴
| MN |
| AC |
| EN |
| EC |
∵AB的长为10cm,MN=ycm,AC=xcm.
∴
| y |
| x |
| 10-x-y |
| 10-x |
| 1 |
| 10 |
②∵由①可知,y=-
| 1 |
| 10 |
| 1 |
| 10 |
∴当x=5时,MN的值最大,MN的最大长度为2.5cm,即当C点是AB中点时,线段MN的最大长度是2.5cm.
点评:本题考查的是等边三角形的性质、全等三角形的判定与性质、二次函数的最值问题,涉及面较广,难度适中.

练习册系列答案
相关题目
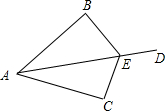 已知:如图,点E是AD上一点,AB=AC,如果AD是∠BAC的平分线.求证:EA是∠BEC的平分线.
已知:如图,点E是AD上一点,AB=AC,如果AD是∠BAC的平分线.求证:EA是∠BEC的平分线. 9、已知:如图,点C是∠AOB的角平分线的一点,CD∥OA交OB于D,CE⊥OA于E,且∠COA=15°,CE=4cm,那么CD=
9、已知:如图,点C是∠AOB的角平分线的一点,CD∥OA交OB于D,CE⊥OA于E,且∠COA=15°,CE=4cm,那么CD= 已知:如图,点O是△ABC的重心,连接AO并延长交BC于点D,则下列命题中正确的是( )
已知:如图,点O是△ABC的重心,连接AO并延长交BC于点D,则下列命题中正确的是( ) 已知,如图,点D是△ABC的两外角平分线的交点,下列说法:
已知,如图,点D是△ABC的两外角平分线的交点,下列说法: 已知:如图,点E是AD上一点,BE=CE,如果∠BEA=∠CEA.
已知:如图,点E是AD上一点,BE=CE,如果∠BEA=∠CEA.