题目内容
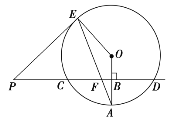
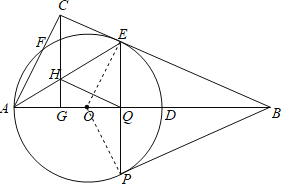
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E,交AC于点F,过点C作CG⊥AB交AB于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为⊙O的切线.
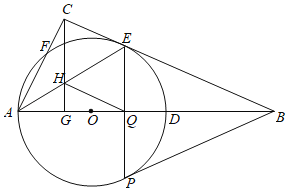
(1)求证:BC是⊙O的切线.
(2)求证:![]() =
=![]() .
.
(3)若sin∠ABC═![]() ,AC=15,求四边形CHQE的面积.
,AC=15,求四边形CHQE的面积.
【答案】(1)见解析;(2)见解析;(3)45
【解析】
(1)连接OE,OP,根据线段垂直平分线的性质得到PB=BE,根据全等三角形的性质得到∠BEO=∠BPO,根据切线的判定和性质定理即可得到结论.
(2)根据平行线和等腰三角形的性质即可得到结论.
(3)根据垂径定理得到EP⊥AB,根据平行线和等腰三角形的性质得到∠CAE=∠EAO,根据全等三角形的性质得到CE=QE,推出四边形CHQE是菱形,解直角三角形得到CG=![]() =12,根据勾股定理即可得到结论.
=12,根据勾股定理即可得到结论.
(1)证明:连接OE,OP,
∵PE⊥AB,点Q为弦EP的中点,
∴AB垂直平分EP,
∴PB=BE,
∵OE=OP,OB=OB,
∴△BEO≌△BPO(SSS),
∴∠BEO=∠BPO,
∵BP为⊙O的切线,
∴∠BPO=90°,
∴∠BEO=90°,
∴OE⊥BC,
∴BC是⊙O的切线.
(2)解:∵∠BEO=∠ACB=90°,
∴AC∥OE,
∴∠CAE=∠OEA,
∵OA=OE,
∴∠EAO=∠AEO,
∴∠CAE=∠EAO,
∴![]() .
.
(3)解:∵AD为的⊙O直径,点Q为弦EP的中点,
∴EP⊥AB,
∵CG⊥AB,
∴CG∥EP,
∵∠ACB=∠BEO=90°,
∴AC∥OE,
∴∠CAE=∠AEO,
∵OA=OE,
∴∠EAQ=∠AEO,
∴∠CAE=∠EAO,
∵∠ACE=∠AQE=90°,AE=AE,
∴△ACE≌△AQE(AAS),
∴CE=QE,
∵∠AEC+∠CAE=∠EAQ+∠AHG=90°,
∴∠CEH=∠AHG,
∵∠AHG=∠CHE,
∴∠CHE=∠CEH,
∴CH=CE,
∴CH=EQ,
∴四边形CHQE是平行四边形,
∵CH=CE,
∴四边形CHQE是菱形,
∵sin∠ABC═sin∠ACG═![]() =
=![]() ,
,
∵AC=15,
∴AG=9,
∴CG=![]() =12,
=12,
∵△ACE≌△AQE,
∴AQ=AC=15,
∴QG=6,
∵HQ2=HG2+QG2,
∴HQ2=(12﹣HQ)2+62,
解得:HQ=![]() ,
,
∴CH=HQ=![]() ,
,
∴四边形CHQE的面积=CHGQ=![]() ×6=45.
×6=45.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案