题目内容
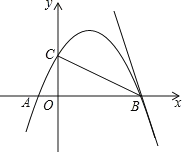
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() 、
、![]() 两点.
两点.![]() 为抛物线上一动点(不与点
为抛物线上一动点(不与点![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方时,过点
上方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,请直接写出点
为顶点的四边形能否构成平行四边形?若能,请直接写出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)能构成,点F的坐标是(2,4)或
;(3)能构成,点F的坐标是(2,4)或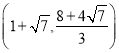 或
或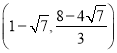 或
或![]() .
.
【解析】
(1)根据待定系数法解答即可;
(2)求出OA和OE的长后易证![]() ,由相似三角形的性质可得
,由相似三角形的性质可得![]() ,于是
,于是![]() 可转化为
可转化为![]() ,只要求出PN的最大值即可,可设点P的横坐标为m,则PN的长可用含m的代数式表示,再利用二次函数的性质即可求出PN的最大值,进一步即可求出结果;
,只要求出PN的最大值即可,可设点P的横坐标为m,则PN的长可用含m的代数式表示,再利用二次函数的性质即可求出PN的最大值,进一步即可求出结果;
(3)分情况讨论:当CE为边时,则CE=PF,CE∥PF,易得CE=2,再分点![]() 在直线
在直线![]() 上方和点
上方和点![]() 在直线
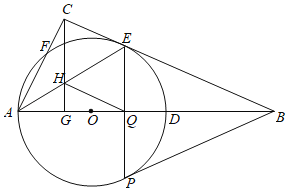
在直线![]() 下方,设点P的横坐标为m,由PF=2可得关于m的方程,解方程即可求出m,进而可求得点F的坐标;当CE为对角线时,如图,则CP=EF,CP∥EF,设点P的横坐标为m,表示出点P、F坐标后,由平行四边形的性质可得
下方,设点P的横坐标为m,由PF=2可得关于m的方程,解方程即可求出m,进而可求得点F的坐标;当CE为对角线时,如图,则CP=EF,CP∥EF,设点P的横坐标为m,表示出点P、F坐标后,由平行四边形的性质可得![]() ,从而可得关于m的方程,解方程即可求出m,进而可求得点F的坐标.
,从而可得关于m的方程,解方程即可求出m,进而可求得点F的坐标.
解(1)![]() 抛物线
抛物线![]() 经过点
经过点![]() ,
,![]() ,
,
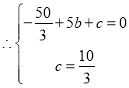 ,解得:
,解得: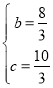 ,
,
∴抛物线的解析式为![]() ;
;
(2)在直线![]() 中,当
中,当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() ,
,
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,
![]() 轴,
轴,![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上方,
上方,
∴![]() ,
,
∴当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ,此时
,此时![]() 的最大值=
的最大值=![]() ;
;
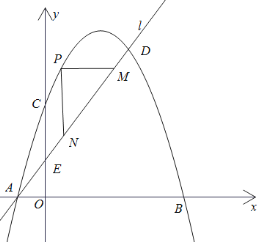
(3)由题意得:当CE为边时,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能构成平行四边形,则CE=PF,CE∥PF,
为顶点的四边形能构成平行四边形,则CE=PF,CE∥PF,
当点![]() 在直线
在直线![]() 上方时,设
上方时,设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,解得:m=0(舍去)或m=2,
,解得:m=0(舍去)或m=2,
此时点F的坐标是(2,4);
当点![]() 在直线
在直线![]() 下方时,
下方时,![]() ,
,
∴![]() ,解得:
,解得:![]() 或
或![]() ,
,
此时点F的坐标是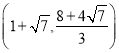 或
或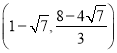 ;
;
当CE为对角线时,如图,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能构成平行四边形,则CP=EF,CP∥EF,
为顶点的四边形能构成平行四边形,则CP=EF,CP∥EF,
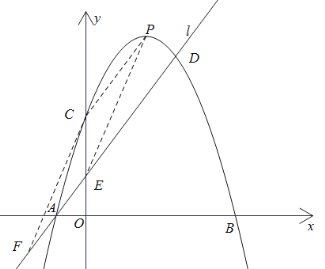
此时可设![]() ,则由
,则由![]() 可得
可得![]() ,
,
由![]() 得:
得:![]() ,
,
解得:m=0(舍去)或m=2,
此时点F的坐标是![]() ;
;
综上所述,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能构成平行四边形,且点F的坐标是(2,4)或
为顶点的四边形能构成平行四边形,且点F的坐标是(2,4)或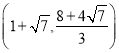 或
或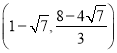 或
或![]() .
.

【题目】为了提高学生身体素质,某市中小学开展阳光健步走活动,某数学兴趣小组收集了某校![]() 名学生一天行走的步数并记录如下:
名学生一天行走的步数并记录如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
对这![]() 个数据按组距
个数据按组距![]() 进行分组,并统计整理,绘制了如下尚不完整的统计图表.
进行分组,并统计整理,绘制了如下尚不完整的统计图表.
调查结果统计表:
组别 | 步数分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
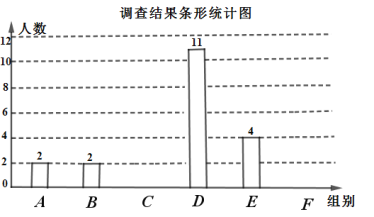
请根据以上信息,解答下列问题:
(1)填空:![]() ,
,![]()
(2)请补全条形统计图.
(3)这![]() 名学生一天行走步数的众数落在 组.
名学生一天行走步数的众数落在 组.
(4)根据科学研究,初中生一天的健步行走应不少于![]() 步,若该校有
步,若该校有![]() 名初中生,请你估计该校一天健步行走不少于
名初中生,请你估计该校一天健步行走不少于![]() 步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)
步的学生人数,并根据上述数据,给校方提出合理化的建议(有利于健步行走的)