题目内容
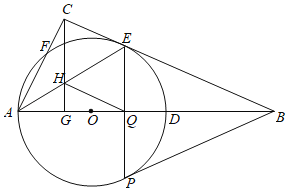
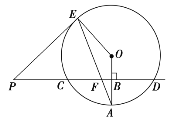
【题目】已知直线PD垂直平分⊙O的半径OA于点B,PD交⊙O于点C、D,PE是⊙O的切线,E为切点,连接AE,交CD于点F.
(1)若⊙O的半径为8,求CD的长;
(2)若PF=13,求PE的长;
(3)在(2)的条件下,sinA=![]() ,求EF的长.
,求EF的长.
【答案】(1)![]() ;(2)13;(3)10
;(2)13;(3)10
【解析】
(1)首先连接OD,由直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,可求得OB的长,又由勾股定理,可求得BD的长,然后由垂径定理,求得CD的长;
(2)由PE是⊙O的切线,易证得∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,继而可证得∠PEF=∠PFE,根据等角对等边的性质,可得PE=PF,求得PE的长;
(3)首先过点P作PG⊥EF于点G,易得∠FPG=∠A,即可得FG=PFsinA=13×![]() =5,又由等腰三角形的性质,求得答案.
=5,又由等腰三角形的性质,求得答案.
解:(1)连接OD,
∵直线PD垂直平分⊙O的半径OA于点B,⊙O的半径为8,
∴OB=![]() OA=4,BC=BD=
OA=4,BC=BD=![]() CD,
CD,
∴在Rt△OBD中,BD=![]()
∴CD=2BD=![]() ;
;
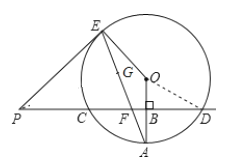
(2)∵PE是⊙O的切线,
∴∠PEO=90°,
∴∠PEF=90°-∠AEO,∠PFE=∠AFB=90°-∠A,
∵OE=OA,
∴∠A=∠AEO,
∴∠PEF=∠PFE,
∴PE=PF=13;
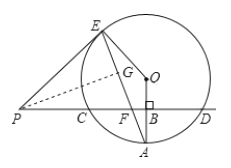
(3)过点P作PG⊥EF于点G,
∴∠PGF=∠ABF=90°,
∵∠PFG=∠AFB,
∴∠FPG=∠A,
∴FG=PFsinA=13×![]() =5
=5
∵PE=PF,
∴EF=2FG=10.

练习册系列答案
相关题目