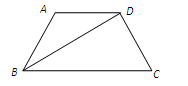
题目内容
如图所示,在□ABCD中,E、F是对角线AC上两点,且AE = CF.求证:四边形DEBF 是平行四边形.
是平行四边形.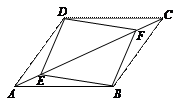
 是平行四边形.
是平行四边形.
证明:连续BD交AC于点O
∵ 四边形ABCD是平行四边形
∴ AO = CD,DO = BO
∵ AE = CF
∴ AO – AE =" CO" – CF,即EO = FO
∴ 四边形EBFD是平等四边形
∵ 四边形ABCD是平行四边形
∴ AO = CD,DO = BO
∵ AE = CF
∴ AO – AE =" CO" – CF,即EO = FO
∴ 四边形EBFD是平等四边形
略

练习册系列答案
相关题目

 中,
中, ,
, 平分
平分 ,
, 交
交 于
于 .
.
 是菱形;
是菱形; 的形状,并说明理由.
的形状,并说明理由. 的对角线相交于点
的对角线相交于点 请你添加一个条件: ,使其为正方形
请你添加一个条件: ,使其为正方形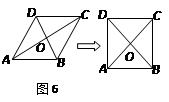

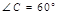 ,BD平分
,BD平分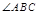 ,如果这个梯形的周长为30,则AB的长为( )
,如果这个梯形的周长为30,则AB的长为( )