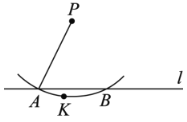
题目内容
【题目】对于平面直角坐标系![]() 中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果
中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果![]() 两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作
两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作![]() .已知直线
.已知直线![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,![]() 的半径为1.
的半径为1.
(1)若![]() ,
,
①求![]() 的值;
的值;
②若点C在直线![]() 上,求
上,求![]() 的最小值;
的最小值;
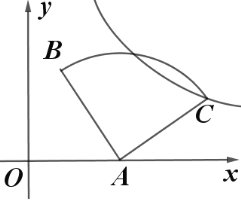
(2)以点A为中心,将线段![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,点E在线段
,点E在线段![]() 组成的图形上,若对于任意点E,总有
组成的图形上,若对于任意点E,总有![]() ,直接写出b的取值范围.
,直接写出b的取值范围.
【答案】(1)①3;②![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)①直接利用圆外一点到圆上的一点的最大距离,即可得出结论;
②先判断出OC⊥AB时,OC最短,即可得出结论;
(2)Ⅰ、当b>0时,当直线AB与⊙O相切时,d(E,⊙O)最小,当点E恰好在点D时,d(E,⊙O)最大,即可得出结论;
Ⅱ、当b<0时,同Ⅰ的方法即可得结论.
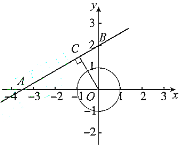
解:(1)①根据题意可知![]() .
.
![]() .
.
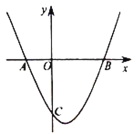
②如图,过点O作![]() 于点C,此时
于点C,此时![]() 取得最小值.
取得最小值.
![]() 直线
直线![]() 与x轴交于点A,
与x轴交于点A,
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() 的最小值为
的最小值为![]() .
.
(2)![]() 或
或![]()
Ⅰ、当b>0时,如图2,
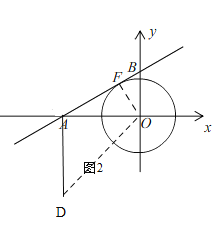
针对于直线y=![]() x+b(b≠0),
x+b(b≠0),
令x=0,则y=b,
∴B(0,b),
∴OB=b,
令y=0,则0=![]() x+b,
x+b,
∴x=![]() b,
b,
∴A(![]() b,0),
b,0),
∴OA=![]() b,
b,
则AB=2b,tan∠OAB=![]() =
=![]() ,
,
∴∠OAB=30°,
由旋转知,AD=AB=2b,∠BAD=120°,
则有∠OAD=90°,
连接OD,
∴OD=![]() =
=![]() b,
b,
∵⊙O的半径为1,
∴当线段AB与⊙O相切时,d(E,⊙O)最小=2,
同(1)的方法得,OF=![]() =1,
=1,
∴b=![]() (舍去负值),
(舍去负值),
对于任意点E,总有2≤d(E,⊙O)<6,
∴![]() b<6-1,
b<6-1,
∴b<![]() ,
,
即![]() ≤b<
≤b<![]() ;
;
Ⅱ、当b<0时,如图3,
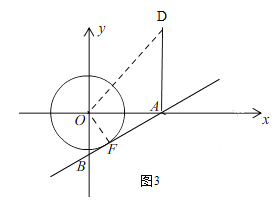
同Ⅰ的方法得,-![]() <b≤-
<b≤-![]() ,
,
综上述,-![]() <b≤-
<b≤-![]() 或
或![]() ≤b<
≤b<![]() .
.

练习册系列答案
相关题目