题目内容
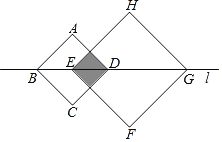
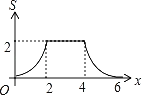
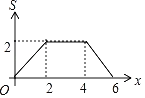
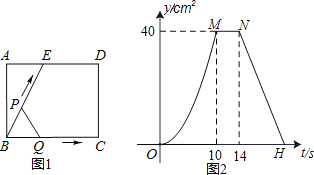
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm)2.已知y与t的函数关系图象如图2,则下列结论错误的是( )
A.AE=6cm
B.sin∠EBC=0.8
C.当 0<t≤10 时,y=0.4t2
D.当 t=12s 时,△PBQ 是等腰三角形
【答案】D
【解析】
根据函数图象可知在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数;在ED段,y=40是定值,持续时间4s,则ED=4;在DC段,y持续减小直至为0,y是t的一次函数.
解: A正确.理由如下:
分析函数图象可知,BC=10cm,ED=4cm,故AE=AD-ED=BC-ED=10-4=6cm;
B正确.理由如下:
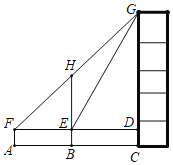
如图所示,连接EC,过点E作EF⊥BC于点F,
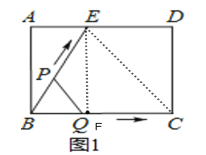
由函数图象可知,![]() ,
,
∴EF=8,
∴![]() ;
;
C正确.理由如下:
如图所示,过点P作PG⊥BQ于点G,
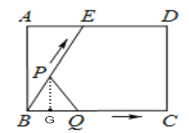
∵BQ=BP=t,
∴![]() .
.
D错误.理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,设为N,如图所示,连接NB,NC.
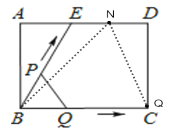
此时AN=8,ND=2,由勾股定理求得:![]() ,
,
∵BC=10,
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形.
故选:D.

 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案【题目】某校随机抽查了部分九年级女生进行1分钟仰卧起坐测试,并将测试的结果绘制成了如图的不完整的统计表和频数分布直方图(注:在频数分布直方图中,每组含左端点,但不含右端点):
仰卧起坐次数的范围(次) | 15~20 | 20~25 | 25~30 | 30~35 |
频数 | 3 | 10 | 12 |
|
频率 |
|
|
|
|

(1)30~35的频数是 、25~30的频率是 .并把统计图补充完整;
(2)被抽查的所有女同学仰卧起坐次数的中位数是多少?