ÌâÄ¿ÄÚÈÝ
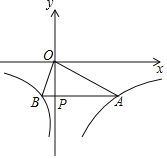
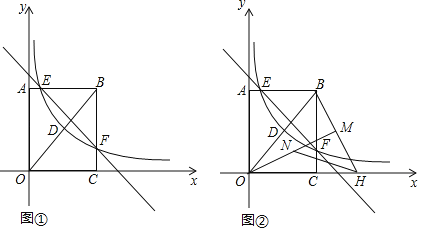
¡ŸÌâÄ¿¡¿ÈçÍŒ¢Ù£¬ÔÚŸØÐÎOABCÖУ¬OA£œ4£¬OC£œ3£¬·Ö±ðÒÔOC¡¢OAËùÔÚµÄÖ±ÏßΪxÖá¡¢yÖᣬœšÁ¢ÈçÍŒËùÊŸµÄ×ø±êϵ£¬Á¬œÓOB£¬·Ž±ÈÀýº¯Êýy£œ![]() £šx£Ÿ0£©µÄÍŒÏóŸ¹ýÏ߶ÎOBµÄÖеãD£¬²¢ÓëŸØÐεÄÁœ±ßœ»ÓÚµãEºÍµãF£¬Ö±Ïßl£ºy£œkx+bŸ¹ýµãEºÍµãF£®
£šx£Ÿ0£©µÄÍŒÏóŸ¹ýÏ߶ÎOBµÄÖеãD£¬²¢ÓëŸØÐεÄÁœ±ßœ»ÓÚµãEºÍµãF£¬Ö±Ïßl£ºy£œkx+bŸ¹ýµãEºÍµãF£®
£š1£©Ç󷎱ÈÀýº¯ÊýµÄœâÎöÊœ£»
£š2£©Á¬œÓOE¡¢OF£¬Çó¡÷OEFµÄÃæ»ý£»
£š3£©ÔÚµÚÒ»ÏóÏÞÄÚ£¬ÇëÖ±œÓÐŽ³ö¹ØÓÚxµÄ²»µÈÊœkx+b¡Ü![]() µÄœâŒ¯£º¡¡ £®
µÄœâŒ¯£º¡¡ £®
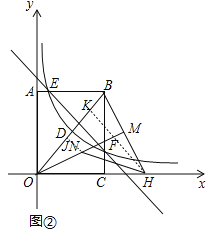
£š4£©ÈçÍŒ¢Ú£¬œ«Ï߶ÎOBÈƵãO˳ʱÕëÐýתһ¶šœÇ¶È£¬Ê¹µÃµãBµÄ¶ÔÓŠµãHÇ¡ºÃÂäÔÚxÖáµÄÕý°ëÖáÉÏ£¬Á¬œÓBH£¬×÷OM¡ÍBH£¬µãNΪÏ߶ÎOMÉϵÄÒ»žö¶¯µã£¬ÇóHN+![]() ONµÄ×îСֵ£®
ONµÄ×îСֵ£®
¡ŸŽð°ž¡¿£š1£©y£œ![]() £»£š2£©S¡÷OEF£œ
£»£š2£©S¡÷OEF£œ![]() £»£š3£©0£Œx£Œ
£»£š3£©0£Œx£Œ![]() »òx£Ÿ3£®£š4£©HN+
»òx£Ÿ3£®£š4£©HN+![]() ONµÄ×îСֵΪ4£®
ONµÄ×îСֵΪ4£®
¡ŸœâÎö¡¿
£š1£©Ê×ÏÈÈ·¶šµãB×ø±ê£¬ÔÙžùŸÝÖеã×ø±ê¹«ÊœÇó³öµãDµÄ×ø±êŒŽ¿ÉœâŸöÎÊÌ⣮
£š2£©Çó³öµãE£¬FµÄ×ø±ê£¬ÔÙžùŸÝS¡÷OEF=SŸØÐÎABCO-S¡÷AOE-S¡÷OCF-S¡÷EFBŒÆË㌎¿É£®
£š3£©ÐŽ³öÔÚµÚÒ»ÏóÏÞ£¬Ö±ÏßµÄÍŒÏóÔÚ·Ž±ÈÀýº¯ÊýµÄÍŒÏóµÄÏ·œµÄ×Ô±äÁ¿xµÄÈ¡Öµ·¶Î§ŒŽ¿É£®
£š4£©ÈçÍŒ¢ÚÖУ¬×÷NJ¡ÍBDÓÚJ£®HK¡ÍBDÓÚK£®œâÖ±œÇÈýœÇÐÎÊ×ÏÈÖ€Ã÷£ºsin¡ÏNOD=![]() £¬ÍƳöNJ=ONsin¡ÏNOD=
£¬ÍƳöNJ=ONsin¡ÏNOD=![]() ON£¬ÍƳöNH+
ON£¬ÍƳöNH+![]() ON=NH+NJ£¬žùŸÝŽ¹Ï߶Î×î¶Ì¿ÉÖª£¬µ±J£¬N£¬H¹²Ïߣ¬ÇÒÓëHKÖغÏʱ£¬HN+
ON=NH+NJ£¬žùŸÝŽ¹Ï߶Î×î¶Ì¿ÉÖª£¬µ±J£¬N£¬H¹²Ïߣ¬ÇÒÓëHKÖغÏʱ£¬HN+![]() ONµÄÖµ×îС£¬×îСֵ=HKµÄ³€£¬ÓÉŽËŒŽ¿ÉœâŸöÎÊÌ⣮
ONµÄÖµ×îС£¬×îСֵ=HKµÄ³€£¬ÓÉŽËŒŽ¿ÉœâŸöÎÊÌ⣮
œâ£º£š1£©ÔÚŸØÐÎABCOÖУ¬¡ßOA£œBC£œ4£¬OC£œAB£œ3£¬
¡àB£š3£¬4£©£¬
¡ßOD£œDB£¬
¡àD£š![]() £¬2£©£¬
£¬2£©£¬
¡ßy£œ![]() Ÿ¹ýD£š
Ÿ¹ýD£š![]() £¬2£©£¬
£¬2£©£¬
¡àk£œ3£¬
¡à·Ž±ÈÀýº¯ÊýµÄœâÎöʜΪy£œ![]() £®
£®
£š2£©ÈçÍŒ¢ÙÖУ¬Á¬œÓOE£¬OF£®
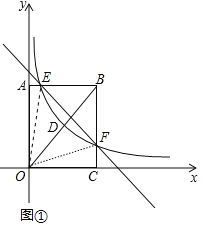
ÓÉÌâÒâE£š![]() £¬4£©£¬F£š3£¬1£©£¬
£¬4£©£¬F£š3£¬1£©£¬
¡àS¡÷OEF£œSŸØÐÎABCO©S¡÷AOE©S¡÷OCF©S¡÷EFB
£œ12©![]() ¡Á4¡Á
¡Á4¡Á![]() ©
©![]() ¡Á3¡Á1©
¡Á3¡Á1©![]() ¡Á3¡Á£š3©
¡Á3¡Á£š3©![]() £©
£©
£œ![]() £®
£®
£š3£©¹Û²ìÍŒÏó¿ÉÖª£ºÔÚµÚÒ»ÏóÏÞÄÚ£¬¹ØÓÚxµÄ²»µÈÊœkx+b¡Ü![]() µÄœâŒ¯Îª£º0£Œx£Œ
µÄœâŒ¯Îª£º0£Œx£Œ![]() »òx£Ÿ3£®
»òx£Ÿ3£®
¹ÊŽð°žÎª£º0£Œx£Œ![]() »òx£Ÿ3£®
»òx£Ÿ3£®
£š4£©ÈçÍŒ¢ÚÖУ¬×÷NJ¡ÍBDÓÚJ£®HK¡ÍBDÓÚK£®
ÓÉÌâÒâOB£œOH£œ5£¬
¡àCH£œOH©OC£œ5©3£œ2£¬
¡àBH£œ![]() £œ
£œ![]() £œ2
£œ2![]() £¬
£¬
¡àsin¡ÏCBH£œ![]() £œ
£œ![]() £¬
£¬
¡ßOM¡ÍBH£¬
¡à¡ÏOMH£œ¡ÏBCH£œ90¡ã£¬
¡ß¡ÏMOH+¡ÏOHM£œ90¡ã£¬¡ÏCBH+¡ÏCHB£œ90¡ã£¬
¡à¡ÏMOH£œ¡ÏCBH£¬
¡ßOB£œOH£¬OM¡ÍBH£¬
¡à¡ÏMOB£œ¡ÏMOH£œ¡ÏCBH£¬
¡àsin¡ÏNOD£œ![]() £¬
£¬
¡àNJ£œONsin¡ÏNOD£œ![]() ON£¬
ON£¬
¡àNH+![]() ON£œNH+NJ£¬
ON£œNH+NJ£¬
žùŸÝŽ¹Ï߶Î×î¶Ì¿ÉÖª£¬µ±J£¬N£¬H¹²Ïߣ¬ÇÒÓëHKÖغÏʱ£¬HN+![]() ONµÄÖµ×îС£¬×îСֵ£œHKµÄ³€£¬
ONµÄÖµ×îС£¬×îСֵ£œHKµÄ³€£¬
¡ßOB£œOH£¬BC¡ÍOH£¬HK¡ÍOB£¬
¡àHK£œBC£œ4£¬
¡àHN+![]() ONÊÇ×îСֵΪ4£®
ONÊÇ×îСֵΪ4£®

 ʱ¿Ì׌±ž×ÅÊîŒÙ×÷ÒµÔ×ÓÄܳö°æÉçϵÁÐŽð°ž
ʱ¿Ì׌±ž×ÅÊîŒÙ×÷ÒµÔ×ÓÄܳö°æÉçϵÁÐŽð°ž ÊîŒÙÏΜӜ̲ÄÆÚÄ©ÊîŒÙԀϰÎ人³ö°æÉçϵÁÐŽð°ž
ÊîŒÙÏΜӜ̲ÄÆÚÄ©ÊîŒÙԀϰÎ人³ö°æÉçϵÁÐŽð°ž ŒÙÆÚ×÷ÒµÊîŒÙ³É³€ÀÖÔ°ÐÂœ®ÇàÉÙÄê³ö°æÉçϵÁÐŽð°ž
ŒÙÆÚ×÷ÒµÊîŒÙ³É³€ÀÖÔ°ÐÂœ®ÇàÉÙÄê³ö°æÉçϵÁÐŽð°ž