题目内容
已知抛物线的顶点坐标为(
,-
),且经过点C(1,0),若此抛物线与x轴的另一交点为点B,与y轴的交点为点A,设P、Q分别为AB、OB边上的动点,它们同时分别从点A、O向B点匀速运动,速度均为每秒1个单位,设P、Q移动时间为t(0≤t≤4)
(1)求此抛物线的解析式并求出P点的坐标(用t表示);
(2)当△OPQ面积最大时求△OBP的面积;
(3)当t为何值时,△OPQ为直角三角形?
(4)△OPQ是否可能为等边三角形?若可能请求出t的值;若不可能请说明理由,并改变点Q的运动速度,使△OPQ为等边三角形,求出此时Q点运动的速度和此时t的值.

| 5 |
| 2 |
| 27 |
| 16 |
(1)求此抛物线的解析式并求出P点的坐标(用t表示);
(2)当△OPQ面积最大时求△OBP的面积;
(3)当t为何值时,△OPQ为直角三角形?
(4)△OPQ是否可能为等边三角形?若可能请求出t的值;若不可能请说明理由,并改变点Q的运动速度,使△OPQ为等边三角形,求出此时Q点运动的速度和此时t的值.

(1)设抛物线的解析式为:y=a(x-
)2-
,代入点(1,0),得:a=
;
∴y=
(x-
)2-
.
令y=0得:x1=4,x2=1,∴B(4,0).
令x=0得:y=3,∴A(0,3),AB=5.
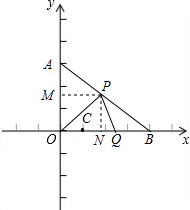 如右图,过点P作PM⊥y轴,垂足为点M,则:
如右图,过点P作PM⊥y轴,垂足为点M,则:
=
=
,得:
=
=
∴AM=
t,PM=
t
∴P(
t,3-
t).
(2)如图,过点P作PN⊥x轴,垂足为点N,
S△OPQ=
OQ•PN=
t•(3-
t)=
t-
t2=-
(t-
)2+
∴当t=
时,S△OPQ最大=
.
此时OP为AB边上的中线
∴S△OBP=
S△AOB=
×
×3×4=3.
(3)若∠OQP=90°,则
=
,
∴
=
,得t=0(舍去).
若∠OPQ=90°,则OP2+PQ2=OQ2,
∴(3-
t)2+(
t)2+(3-
t)2+(
t)2=t2
解得:t1=3,t2=15(舍去).
当t=3时,△OPQ为直角三角形.
(4)∵OP2=(3-
t)2+(
t)2,PQ2=(3-
t)2+(
t)2;
∴OP≠PQ,
∴△OPQ不可能是等边三角形.
设Q点的速度为每秒k个单位时,△OPQ为等边三角形
∴kt=2•
t,得 k=
∵PN=
OP=
•
t=
t
∴3-
t=
t,得t=
.
| 5 |
| 2 |
| 27 |
| 16 |
| 3 |
| 4 |
∴y=
| 3 |
| 4 |
| 5 |
| 2 |
| 27 |
| 16 |
令y=0得:x1=4,x2=1,∴B(4,0).
令x=0得:y=3,∴A(0,3),AB=5.
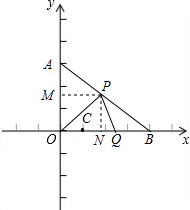 如右图,过点P作PM⊥y轴,垂足为点M,则:
如右图,过点P作PM⊥y轴,垂足为点M,则:| AM |
| AO |
| PM |
| OB |
| AP |
| AB |
| AM |
| 3 |
| PM |
| 4 |
| t |
| 5 |
∴AM=
| 3 |
| 5 |
| 4 |
| 5 |
∴P(
| 4 |
| 5 |
| 3 |
| 5 |
(2)如图,过点P作PN⊥x轴,垂足为点N,
S△OPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 2 |
| 3 |
| 10 |
| 3 |
| 10 |
| 5 |
| 2 |
| 15 |
| 8 |
∴当t=
| 5 |
| 2 |
| 15 |
| 8 |
此时OP为AB边上的中线
∴S△OBP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)若∠OQP=90°,则
| BP |
| AB |
| BQ |
| BO |
∴
| 5-t |
| 5 |
| 4-t |
| 4 |
若∠OPQ=90°,则OP2+PQ2=OQ2,
∴(3-
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
解得:t1=3,t2=15(舍去).
当t=3时,△OPQ为直角三角形.
(4)∵OP2=(3-
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
∴OP≠PQ,
∴△OPQ不可能是等边三角形.
设Q点的速度为每秒k个单位时,△OPQ为等边三角形
∴kt=2•
| 4 |
| 5 |
| 8 |
| 5 |
∵PN=
| ||
| 2 |
| ||
| 2 |
| 8 |
| 5 |
4
| ||
| 5 |
∴3-
| 3 |
| 5 |
4
| ||
| 5 |
20
| ||
| 13 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).
绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图). 标;若不存在,请说明理由.(注意:本题中的结果均保留根号)
标;若不存在,请说明理由.(注意:本题中的结果均保留根号)