��Ŀ����
��ͼ����ֱ������ϵ�У��Ե�M��3��0��ΪԲ�ģ���6Ϊ�뾶��Բ�ֱ�x����������ڵ�A����x��ĸ����ύ�ڵ�B����y����������ڵ�C������C��ֱ�߽�x��ĸ������ڵ�D��-9��0��
��1����A��C��������ꣻ
��2����֤��ֱ��CD�ǡ�M�����ߣ�
��3����������y=x2+bx+c����M��A���㣬��������ߵĽ���ʽ��
��4������AC������3���������ߵĶԳ���ֱ���ֱ��CD���ڵ�E����AC���ڵ�F�������P���������ϵĶ��㣬�Ƿ���������ĵ�P��ʹ��S��PAM��S��CEF=
��3�������ڣ��������ʱ��P���� �ꣻ�������ڣ���˵�����ɣ���ע�⣺�����еĽ�����������ţ�
�ꣻ�������ڣ���˵�����ɣ���ע�⣺�����еĽ�����������ţ�
��1����A��C��������ꣻ
��2����֤��ֱ��CD�ǡ�M�����ߣ�
��3����������y=x2+bx+c����M��A���㣬��������ߵĽ���ʽ��
��4������AC������3���������ߵĶԳ���ֱ���ֱ��CD���ڵ�E����AC���ڵ�F�������P���������ϵĶ��㣬�Ƿ���������ĵ�P��ʹ��S��PAM��S��CEF=
| 3 |
 �ꣻ�������ڣ���˵�����ɣ���ע�⣺�����еĽ�����������ţ�
�ꣻ�������ڣ���˵�����ɣ���ע�⣺�����еĽ�����������ţ���1������CM��������ã�OM=3��OB=3��OE=9��MC=6
OA=OM+MA=3+6=9
A��9��0��
��OC=
=3
��C��0��3
��
��2��֤��һ��
��Rt��DCO����DC=
=6
�ڡ�DCM�У���CM2+DC2=144
DM2=��DO+OM��2=��9+3��2=122=144
��CM2+DC2=DM2
���DCMֱ�������Σ�
��MC��DC����MC�ǡ�M�İ뾶
��CD�ǡ�M�����ߣ�
֤������
��Rt��COM����sin��MCO=
=
��
���MCO=30��
��Rt��DOC����tan��DCO=
=
=
��
���DCO=60��
���DCM=��MCO+��DCO=90��
��MC��DC����MC�еġ�M�뾶��
��3����������y=x2+bx+c������M��3��0���͵�A��9��0�����ɵã�
��ã�
�������ߵĽ���ʽΪ��y=x2-12x+27��
��4������
�������ߵĶԳ��ύx���ڵ�H
�ڣ�2������֤��
���DCO=60�㣬��CDO=30��
�������ߵĶԳ���ƽ����y��
���CEF=��DCO=60��
��OD=OA=9��
��CO��ֱƽ��AD
���CAO=��CDO=30��
��Rt��AFH����AFH=60��
���EFC=60��
���CEF�ǵȱ�������
����C��CG��EF�ڵ�G����CG=6
�ɵã�EF=4
��S��CEF=
EF•CG=
��4
��6=12
��
����P������Ϸ������P����Ϊ��x��y����S��PAM=
AM•y=3y��S��PAM��S��CEF=
��3
��3y��12
=
��3��
��ã�y=4��
��y=4ʱ����x2-12x+27=4�����x=6��
��P��6-
��4����6+
��4����
������P��x���ϣ����P���M�����A�غϣ���ʱ�����������Σ�
������P��x���·������P������Ϊ��x��y��
S��PAM=
AM•��-y��=-3y��S��PAM��S��CEF=
��3
��-3y��12
=
��3
��ã�y=-4
��y=-4ʱ����x2-12x+27=-4�����x=6��
��
��P��6-
��-4����6+
��-4����
�������ĵ㹲��4����
��P��6-
��4����6+
��4����6-
��-4����6+
��-4����
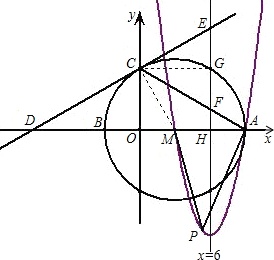
OA=OM+MA=3+6=9
A��9��0��
��OC=
| MC2-OM2 |
| 3 |
��C��0��3
| 3 |
��2��֤��һ��
��Rt��DCO����DC=
| DO2+CO2 |
| 3 |
�ڡ�DCM�У���CM2+DC2=144
DM2=��DO+OM��2=��9+3��2=122=144
��CM2+DC2=DM2
���DCMֱ�������Σ�
��MC��DC����MC�ǡ�M�İ뾶
��CD�ǡ�M�����ߣ�
֤������
��Rt��COM����sin��MCO=
| OM |
| CM |
| 1 |
| 2 |
���MCO=30��
��Rt��DOC����tan��DCO=
| DO |
| CO |
| 9 | ||
3
|
| 3 |
���DCO=60��
���DCM=��MCO+��DCO=90��
��MC��DC����MC�еġ�M�뾶��
��3����������y=x2+bx+c������M��3��0���͵�A��9��0�����ɵã�
|
��ã�
|
�������ߵĽ���ʽΪ��y=x2-12x+27��
��4������
�������ߵĶԳ��ύx���ڵ�H
�ڣ�2������֤��
���DCO=60�㣬��CDO=30��
�������ߵĶԳ���ƽ����y��
���CEF=��DCO=60��
��OD=OA=9��
��CO��ֱƽ��AD
���CAO=��CDO=30��
��Rt��AFH����AFH=60��
���EFC=60��
���CEF�ǵȱ�������
����C��CG��EF�ڵ�G����CG=6
�ɵã�EF=4
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
����P������Ϸ������P����Ϊ��x��y����S��PAM=
| 1 |
| 2 |
| 3 |
��3y��12
| 3 |
| 3 |
��ã�y=4��
��y=4ʱ����x2-12x+27=4�����x=6��
| 13 |
��P��6-
| 13 |
| 13 |
������P��x���ϣ����P���M�����A�غϣ���ʱ�����������Σ�
������P��x���·������P������Ϊ��x��y��
S��PAM=
| 1 |
| 2 |
| 3 |
��-3y��12
| 3 |
| 3 |
��ã�y=-4
��y=-4ʱ����x2-12x+27=-4�����x=6��
| 5 |
��P��6-
| 5 |
| 5 |
�������ĵ㹲��4����
��P��6-
| 13 |
| 13 |
| 5 |
| 5 |
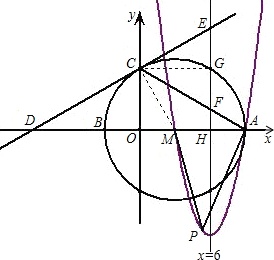

��ϰ��ϵ�д�
 ȫ��������ϵ�д�
ȫ��������ϵ�д�
�����Ŀ
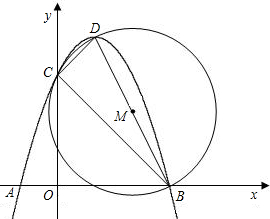 �ڵ�C������ΪD����BDΪֱ���ġ�Mǡ�ù���C��
�ڵ�C������ΪD����BDΪֱ���ġ�Mǡ�ù���C��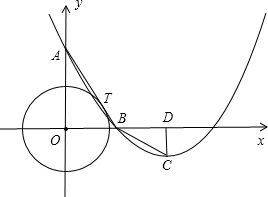 A��0��4������O�����߽�x���ڵ�B��T���е㣬������y=ax2+bx+c�Ķ���ΪC��3��-
A��0��4������O�����߽�x���ڵ�B��T���е㣬������y=ax2+bx+c�Ķ���ΪC��3��-

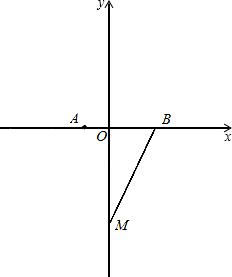 ��M��y��ĸ������ϣ���|AB|=6��cos��OBM=
��M��y��ĸ������ϣ���|AB|=6��cos��OBM=