题目内容
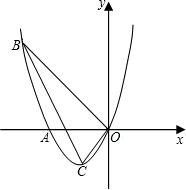
如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-2,-4),O(0,0),B(2,0)三点.
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.
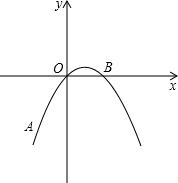
(1)求抛物线y=ax2+bx+c的解析式;
(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.

(1)把A(-2,-4),O(0,0),B(2,0)三点的坐标代入y=ax2+bx+c中,得
解这个方程组,得a=-
,b=1,c=0
所以解析式为y=-
x2+x.
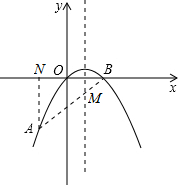
(2)由y=-
x2+x=-
(x-1)2+
,可得
抛物线的对称轴为直线x=1,并且对称轴垂直平分线段OB
∴OM=BM
∴OM+AM=BM+AM
连接AB交直线x=1于M点,则此时OM+AM最小
过点A作AN⊥x轴于点N,
在Rt△ABN中,AB=
=
=4
,
因此OM+AM最小值为4
.
|
解这个方程组,得a=-
| 1 |
| 2 |
所以解析式为y=-
| 1 |
| 2 |
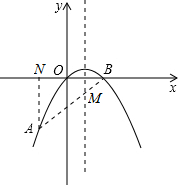
(2)由y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
抛物线的对称轴为直线x=1,并且对称轴垂直平分线段OB
∴OM=BM
∴OM+AM=BM+AM
连接AB交直线x=1于M点,则此时OM+AM最小
过点A作AN⊥x轴于点N,
在Rt△ABN中,AB=
| AN2+BN2 |
| 42+42 |
| 2 |
因此OM+AM最小值为4
| 2 |

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
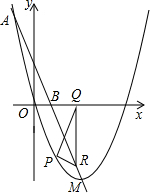
 正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
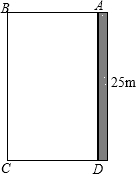 带一边靠墙,另三边用总长为40m的栅栏围住(如图4).若设绿化带的BC边长为xm,绿化带的面积为ym2.
带一边靠墙,另三边用总长为40m的栅栏围住(如图4).若设绿化带的BC边长为xm,绿化带的面积为ym2.