题目内容
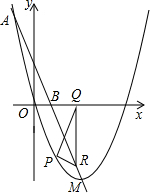
在矩形ABCD中,AB=4,BC=2,以A为坐标原点,AB所在的直线为x轴,建立直角坐标系.然后将矩形ABCD 绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).
绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).
(1)求经过B,E,G三点的二次函数解析式;
(2)设直线EF与(1)的二次函数图象相交于另一点H,试求四边形EGBH的周长.
(3)设P为(1)的二次函数图象上的一点,BP∥EG,求P点的坐标.
 绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).
绕点A逆时针旋转,使点B落在y轴的E点上,则C和D点依次落在第二象限的F点上和x轴的G点上(如图).(1)求经过B,E,G三点的二次函数解析式;
(2)设直线EF与(1)的二次函数图象相交于另一点H,试求四边形EGBH的周长.
(3)设P为(1)的二次函数图象上的一点,BP∥EG,求P点的坐标.
(1)由题意可知,AE=AB=4,AG=AD=BC=2.
∴B(4,0),E(0,4),G(-2,0).
设经过B,E,G三点的二次函数解析式是y=a(x+2)(x-4).
把E(0,4)代入之,求得a=-
.
∴所求的二次函数解析式是:y=-
(x+2)(x-4)=-
x2+x+4.
(2)由题意可知,四边形AEFG为矩形.
∴FH∥GB,且GB=6.
∵直线y=4与二次函数图象的交点H的坐标为H(2,4),
∴EH=2.
∵G与B,E与H关于抛物线的对称轴对称,
∴BH=EG=
=2
.
∴四边形EGBH的周长
=2+6+2×2
=8+4
.
(3)易知直线EG的解析式为y=2x+4,
可是直线PB的解析式为y=2x+h,
则有8+h=0,h=-8;
∴直线BP的解析式为y=2x-8;
联合一次,二次函数解析式组成方程组
,
解得
或
(此组数为B点坐标)
∴所求的P点坐标为P(-6,-20).
∴B(4,0),E(0,4),G(-2,0).
设经过B,E,G三点的二次函数解析式是y=a(x+2)(x-4).
把E(0,4)代入之,求得a=-
| 1 |
| 2 |
∴所求的二次函数解析式是:y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)由题意可知,四边形AEFG为矩形.
∴FH∥GB,且GB=6.
∵直线y=4与二次函数图象的交点H的坐标为H(2,4),
∴EH=2.
∵G与B,E与H关于抛物线的对称轴对称,
∴BH=EG=
| 42+22 |
| 5 |
∴四边形EGBH的周长
=2+6+2×2
| 5 |
=8+4
| 5 |
(3)易知直线EG的解析式为y=2x+4,
可是直线PB的解析式为y=2x+h,
则有8+h=0,h=-8;
∴直线BP的解析式为y=2x-8;
联合一次,二次函数解析式组成方程组
|
解得
|
|
∴所求的P点坐标为P(-6,-20).


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

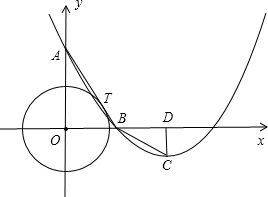 A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-
A(0,4)作⊙O的切线交x轴于点B,T是切点,抛物线y=ax2+bx+c的顶点为C(3,-