题目内容
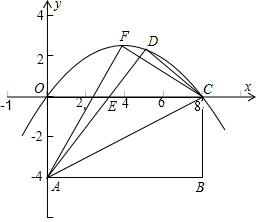
如图抛物线y=-
x2-
x+
,x轴于A、B两点,交y轴于点C,顶点为D.
(1)求A、B、C的坐标;
(2)把△ABC绕AB的中点M旋转180°,得到四边形AEBC:
①求E点坐标;
②试判断四边形AEBC的形状,并说明理由;
(3)试探索:在直线BC上是否存在一点P,使得△PAD的周长最小?若存在,请求出P点的坐标;若不存在,请说明理由.

| ||
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
(1)求A、B、C的坐标;
(2)把△ABC绕AB的中点M旋转180°,得到四边形AEBC:
①求E点坐标;
②试判断四边形AEBC的形状,并说明理由;
(3)试探索:在直线BC上是否存在一点P,使得△PAD的周长最小?若存在,请求出P点的坐标;若不存在,请说明理由.

(1)y=-
x2-
x+
,
令x=0,得y=
令y=0,
即-
x2-
x+
=0,
即x2+2x-3=0,
∴x1=1,x2=-3
∴A,B,C三点的坐标分别为A(-3,0),B(1,0),C(0,
)(3分)
(2)①过点E作EF⊥AB于F,
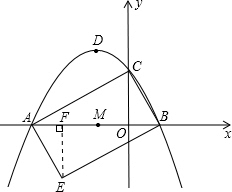 ∵C(0,
∵C(0,
),
∴EF=
,
∵B(1,0),
∴AF=1,
∴OF=OA-AF=3-1=2,
∴E(-2,-
)(5分)
②四边形AEBC是矩形.
理由:四边形AEBC是平行四边形,且∠ACB=90°(7分)
(3)存在.(8分)
D(-1,
)
作出点A关于BC的对称点A′,连接A′D与直线BC交于点P.
 则点P是使△PAD周长最小的点.(10分)
则点P是使△PAD周长最小的点.(10分)
∵AO=3,
∴FO=3,
CO=
,
∴A′F=2
,
∴求得A′(3,2
)
过A′、D的直线y=
x+
过B、C的直线y=-
x+
两直线的交点P(-
,
).(12分)
| ||
| 3 |
2
| ||
| 3 |
| 3 |
令x=0,得y=
| 3 |
令y=0,
即-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
即x2+2x-3=0,
∴x1=1,x2=-3
∴A,B,C三点的坐标分别为A(-3,0),B(1,0),C(0,
| 3 |
(2)①过点E作EF⊥AB于F,
 ∵C(0,
∵C(0,| 3 |
∴EF=
| 3 |
∵B(1,0),
∴AF=1,
∴OF=OA-AF=3-1=2,
∴E(-2,-
| 3 |
②四边形AEBC是矩形.
理由:四边形AEBC是平行四边形,且∠ACB=90°(7分)
(3)存在.(8分)
D(-1,
4
| ||
| 3 |
作出点A关于BC的对称点A′,连接A′D与直线BC交于点P.
 则点P是使△PAD周长最小的点.(10分)
则点P是使△PAD周长最小的点.(10分)∵AO=3,
∴FO=3,
CO=
| 3 |
∴A′F=2
| 3 |
∴求得A′(3,2
| 3 |
过A′、D的直线y=
| ||
| 6 |
3
| ||
| 2 |
过B、C的直线y=-
| 3 |
| 3 |
两直线的交点P(-
| 3 |
| 7 |
10
| ||
| 7 |

练习册系列答案
相关题目