Question

【题目】已知抛物线C：y＝ax2﹣2ax+3开口向下．

（1）当抛物线C过点（1，4）时，求a的值和抛物线与y轴的交点坐标；

（2）求二次函数y＝ax2﹣2ax+3的对称轴和最大值（用含a的式子表示）；

（3）将抛物线C向左平移a个单位得到抛物线C1，随着a的变化，抛物线C1顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；

（4）记（3）所求的函数为D，抛物线C与函数D的图象交于点M，结合图象，请直接写出点M的纵坐标的取值范围．

Answer 1

【答案】（1）a＝﹣1，（0，3）；（2）对称轴为x＝1，最大值为﹣a+3；（3）y＝x+2（x＞1）；（4）3＜yM＜4

【解析】

（1）将（1，4）代入解析式求出a的值，将x＝0代入解析式求出y的值可得其与y轴的交点坐标；

（2）将函数解析式配方成顶点式即可得出答案；

（3）由题意得出平移后的抛物线C1解析式为y＝a（x﹣1+a）2﹣a+3，据此得出抛物线C1顶点坐标为（1﹣a，﹣a+3），即x＝1﹣a，y＝﹣a+3，求出x﹣y即可得出答案；

（4）由抛物线C和函数D的解析式得出分别过定点（2，4）、（2，3），结合函数图象可得答案．

解：（1）抛物线C：y＝ax2﹣2ax+3过点（1，4），

∴a﹣2a+3＝4，

解得a＝﹣1，

当x＝0时，y＝3，即抛物线与y轴的交点为（0，3）；

（2）∵y＝ax2﹣2ax+3＝a（x﹣1）2﹣a+3，抛物线有最高点，

∴二次函数y＝ax2﹣2ax+3的对称轴为x＝1，最大值为﹣a+3；

（3）∵抛物线C：y＝a（x﹣1）2﹣a+3，

∴平移后的抛物线C1：y＝a（x﹣1+a）2﹣a+3，

∴抛物线C1顶点坐标为（1﹣a，﹣a+3），

∴x＝1﹣a，y＝﹣a+3，

∴x﹣y＝1﹣a+a﹣3＝﹣2，

即x﹣y＝﹣2，

∴y＝x+2，

∵a＜0，a＝1﹣x，

∴1﹣x＜0，

∴x＞1，

∴y与x的函数关系式为y＝x+2（x＞1）；

（4）如图，

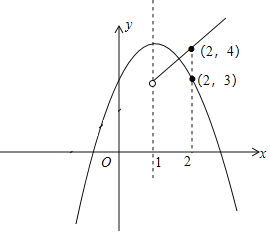
在y＝x+2中，当x＝2时，y＝4，即直线y＝x+2横过点（2，4），

在y＝ax2﹣2ax+3中，当x＝2时，y＝4a﹣4a+3＝3，即抛物线y＝ax2﹣2ax+3横过点（2，3），

所以由图象知，抛物线C与函数D的图象交点M纵坐标的取值范围为3＜yM＜4．