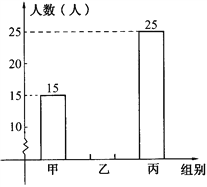
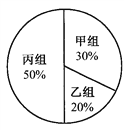
题目内容
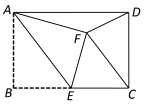
【题目】如图,在矩形ABCD中,AB=4,BC=6,E为BC的中点.将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则△CDF的面积为( )
A. 3.6 B. 4.32 C. 5.4 D. 5.76
【答案】B
【解析】连接BF,过点F作BC的垂线,设△ADF的高为h2,△EFC的高为h1,如图所示:

∵BC=6,点E为BC的中点,
∴BE=3,
又∵AB=4,
∴AE=![]() =5,
=5,
∴BH=![]() ,
,
则BF=![]() ,
,
∵FE=BE=EC,
∴∠BFC=90°,
∴CF=![]() =
=![]()
∴S△BFC=![]()
又∵S△BFC=![]()
∴h1=![]() ,
,
∴S△EFC=![]()
又∵h1+h2=AB=4,
∴h2=![]() ,
,
∴S△ADF=![]() ,
,
∴S△ADF+ S△EFC=![]()
∵S△ABE=6
∴S四边形ABEF=2 S△ABE=12
又∵S矩形ABCD=12
∴S△ADF+ S△EFC+S△CFD=S矩形ABCD-S四边形ABEF=24-12=12
∴S△CFD=12-7.68=4.32;
故选B。

练习册系列答案
相关题目