题目内容
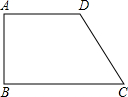 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?分析:根据题意得:AM=tcm,CN=3tcm,又由AD∥BC,可得当AM=BN时,四边形ABNM是平行四边形,即可得方程t=30-3t,解此方程即可求得答案.
解答: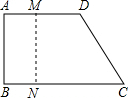 解:根据题意得:AM=tcm,CN=3tcm,
解:根据题意得:AM=tcm,CN=3tcm,
∴BN=BC-CN=30-3t(cm),
∵AD∥BC,
∴当AM=BN时,四边形ABNM是平行四边形,
即t=30-3t,
解得:t=7.5,
故t=7.5,四边形ABNM是平行四边形.
 解:根据题意得:AM=tcm,CN=3tcm,
解:根据题意得:AM=tcm,CN=3tcm,∴BN=BC-CN=30-3t(cm),
∵AD∥BC,
∴当AM=BN时,四边形ABNM是平行四边形,
即t=30-3t,
解得:t=7.5,
故t=7.5,四边形ABNM是平行四边形.
点评:此题考查了梯形的性质与平行四边形的判定.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
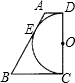 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
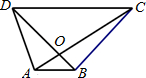 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD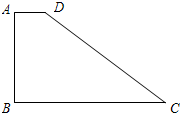 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.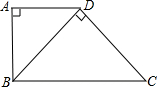 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=