题目内容
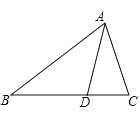
【题目】将一块含有45°的三角板ABC的顶点A放在⊙O上，且AC与⊙O相切于点A（如图1），将△ABC从点A开始，绕着点A顺时针旋转，设旋转角为α（0°＜α＜135°），旋转后，AC、AB分别与⊙O交于点E，F，连接EF（如图2）.已知AC=8，⊙O的半径为4.
（1）在旋转过程中，有以下几个量：①弦EF的长；②
的长；③∠AFE的度数；④点O到EF的距离.其中不变的量是___________________（填序号）；
（2）当α＝________°时，BC与⊙O相切（直接写出答案）；
（3）当BC与⊙O相切时，求△AEF的面积.
【答案】（1）①②④；（2）90°；（3）16
【解析】
试题分析：（1）连接EO，FO，可知三角形EOF为等腰直角三角形，作OD垂直EF于D，由垂径定理，勾股定理可得出结论；（2）因为AC=8，而⊙O的半径为4.所以当BC与⊙O相切时，△ACB绕点A旋转90°后AC恰为⊙O直径，即旋转角α为90度时BC与⊙O相切；（3）当BC与⊙O相切时，如图：点C与点E重合，AC为⊙O直径，利用三角形AEF是等腰直角三角形得出结果.
试题解析：（1）连接EO，FO，因为∠A=45，所以∠EOF=2∠A=90，因为EO=FO，所以三角形EOF为等腰直角三角形，作OD垂直EF于D，由垂径定理得：OD垂直平分EF，三角形ODE和三角形ODF是两个全等的等腰直角三角形，所以EF=
OF，OD=
OF，而半径OF是一定的，所以弦EF的长不变，点O到EF的距离即OD不变，故①④正确，又因为半径不变，圆心角∠EOF=90不变，所以
的长不变，故②正确，而∠AFE的度数等于弧AE度数的一半，A点不变，E是旋转中AC与⊙O交点，可变，故弧AE度数可变，所以∠AFE的度数可变，故③错误，所以不变的序号应是①②④；（2）因为圆的切线垂直于过切点的半径，而∠ACB=90当BC与⊙O相切时，因为AC=8，而⊙O的半径为4.所以△ACB绕点A旋转90°后AC恰为⊙O直径，即旋转角α为90度时BC与⊙O相切；（3）如图，
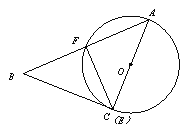
当BC与⊙O相切时，依题意可知，△ACB旋转90°后AC为⊙O直径，且点C与点E重合，∵AC为⊙O直径，∴∠AFE=90°.又∵∠BAC=45°，∴∠FCA=45°.∴∠BAC=∠FCA，∴AF=EF.∵AC=8，∴AF=EF=4
，∴S△AEF=
×（4）2=16.故△AEF的面积是16..
