题目内容
【题目】设函数![]() (
(![]() 为常数),下列说法正确的是( ).
为常数),下列说法正确的是( ).
A. 对任意实数![]() ,函数与
,函数与![]() 轴都没有交点
轴都没有交点
B. 存在实数![]() ,满足当
,满足当![]() 时,函数
时,函数![]() 的值都随
的值都随![]() 的增大而减小
的增大而减小
C. ![]() 取不同的值时,二次函数
取不同的值时,二次函数![]() 的顶点始终在同一条直线上
的顶点始终在同一条直线上
D. 对任意实数![]() ,抛物线
,抛物线![]() 都必定经过唯一定点
都必定经过唯一定点
【答案】D
【解析】试题解析:A. ![]()
∴抛物线的与x轴都有两个交点,故A错误;
B.∵a=1>0,抛物线的对称轴: ![]()
∴在对称轴的左侧函数y的值都随x的增大而减小,
即当x<k时,函数y的值都随x的增大而减小,
当n=k时,当![]() 时,函数y的值都随x的增大而增大,故B错误;
时,函数y的值都随x的增大而增大,故B错误;
C. ![]()
∴抛物线的顶点为![]()
![]() 消去k得,
消去k得, ![]()
由此可见,不论k取任何实数,抛物线的顶点都满足函数![]()
即在二次函数![]() 的图象上.故C错误;
的图象上.故C错误;
D. 令k=1和k=0,得到方程组: ![]() 解得
解得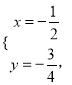
将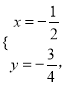 代入
代入![]() 得,
得, ![]() 与k值无关,不论k取何值,抛物线总是经过一个定点
与k值无关,不论k取何值,抛物线总是经过一个定点![]() ,故D正确.
,故D正确.
故选D.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目