ЬтФПФкШн
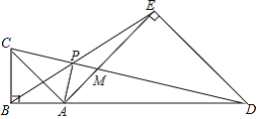
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжагаШ§ЕуAЃЈ2ЃЌ4ЃЉЁЂBЃЈ3ЃЌ5ЃЉЁЂPЃЈaЃЌaЃЉЃЌНЋЯпЖЮABШЦЕуPЫГЪБеыа§зЊ90ЁуЕУЕНCDЃЌЦфжаAЁЂBЕФЖдгІЕуЗжБ№ЮЊCЁЂD;
ЃЈ1ЃЉЕБaЃН2ЪБЃЌ
ЂйдкЭМжаЛГіЯпЖЮCDЃЌБЃСєзїЭМКлМЃЃЌВЂжБНгаДГіCЁЂDСНЕуЕФзјБъЃЛ
ЂкНЋЯпЖЮCDЯђЩЯЦНвЦmИіЕЅЮЛЃЌЕуCЁЂDЧЁКУЭЌЪБТфдкЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЃЌЧѓmКЭkЕФжЕЃЎ
ЕФЭМЯѓЩЯЃЌЧѓmКЭkЕФжЕЃЎ
ЃЈ2ЃЉШєaЃН4ЃЌНЋКЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓШЦЕуPЫГЪБеыа§зЊ90ЁуЕУЕНаТЭМЯѓЃЌжБЯпABгыаТЭМЯѓЕФНЛЕуЮЊEЁЂFЃЌдђEFЕФГЄЮЊЁЁ ЁЁЃЎЃЈжБНгаДГіНсЙћЃЉ
ЃЈxЃО0ЃЉЕФЭМЯѓШЦЕуPЫГЪБеыа§зЊ90ЁуЕУЕНаТЭМЯѓЃЌжБЯпABгыаТЭМЯѓЕФНЛЕуЮЊEЁЂFЃЌдђEFЕФГЄЮЊЁЁ ЁЁЃЎЃЈжБНгаДГіНсЙћЃЉ
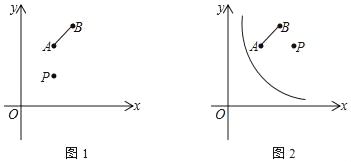
ЁОД№АИЁПЃЈ1ЃЉЂйЭМаЮМћНтЮіЃЛCЃЈ4ЃЌ2ЃЉЃЌDЃЈ5ЃЌ1ЃЉЃЛЂкm=3,k=20;ЃЈ2ЃЉ2![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЛГіЭММДПЩжБЙлЧѓГіЕуЃЛЂкЯђЩЯЦНвЦКсзјБъВЛБфЃЌзнзјБъМгmЃЌдйНсКЯЗДБШКЏЪ§НтЮіЪНСЊСЂЗНГЬЧѓГіmКЭkЃЛ
ЃЈ2ЃЉХаЖЯЭМЯѓа§зЊКѓгыжБЯпЯрНЛЕФНЛЕудкжБЯпЩЯЃЌЖјжБЯпABЩЯЕуШЦPЕуФцЪБеыа§зЊКѓЕФЙьМЃЪЧгыABДЙжБЕФжБЯпЃЌВЂЧвЙ§AЕуЃЌФцЯђЫМЮЌЃЌдЗДБШР§КЏЪ§ЭМЯѓгыЙьМЃжБЯпЕФНЛЕуМфОрРыОЭЪЧEFОрРыЃЎ
ЃЈ1ЃЉЂйИљОнЬтвтзїГіЭМЯѓШчЯТЃК
CЃЈ4ЃЌ2ЃЉЃЌDЃЈ5ЃЌ1ЃЉЃЌ
ЂкCЕуЯђЩЯЦНвЦmИіЕЅЮЛКѓЕузјБъЮЊЃЈ4ЃЌ2+mЃЉЃЌ
DЕуЯђЩЯЦНвЦmИіЕЅЮЛКѓЕузјБъЮЊЃЈ5ЃЌ1+mЃЉЃЌ
ЁпЕуCЁЂDЧЁКУЭЌЪБТфдкЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЃЌ
ЕФЭМЯѓЩЯЃЌ
Ёр4ЃЈ2+mЃЉЃН5ЃЈ1+mЃЉЃЌ
НтЕУmЃН3ЃЌ
ЁрЦНвЦКѓCЕузјБъЮЊЃЈ4ЃЌ5ЃЉЃЌДњШыyЃН![]() ЃЌ
ЃЌ
ЕУЕНkЃН20ЃЛ
ЃЈ2ЃЉЩшжБЯпABЕФНтЮіЪНЪЧyЃНkx+bЃЌНЋЕуAЃЈ2ЃЌ4ЃЉЁЂBЃЈ3ЃЌ5ЃЉДњШыЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯпABНтЮіЪНЮЊyЃНx+2ЃЌ
ЁржБЯпABгыаТЭМЯѓЕФНЛЕудкЙ§AЕугыABДЙжБЕФжБЯпЩЯЃЌ
ЁрИУжБЯпНтЮіЪНЮЊyЃНЉx+6ЃЌ
ЗДБШР§КЏЪ§гыyЃНЉx+6ЕФСННЛЕуЕФОрРыМДЮЊEFЕФОрРыЃЌ
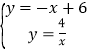 ЃЌ
ЃЌ
Ёрx2Љ6x+4ЃН0ЃЌ
Ёрx1+x2ЃН6ЃЌx1x2ЃН4ЃЌ
ЁрEFЃН![]() |x1Љx2|ЃН2
|x1Љx2|ЃН2![]() ЃЎ
ЃЎ

 КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ
КЃЕэЛЦИдУћЪІЕМКНЯЕСаД№АИ ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИ
ЦеЭЈИпжаЭЌВНСЗЯАВсЯЕСаД№АИЁОЬтФПЁПЮЊКыбяжаЛЊДЋЭГЮФЛЏЃЌФГаЃзщжЏАЫФъМЖ1000УћбЇЩњВЮМгККзжЬ§аДДѓШќЃЎЮЊСЫНтбЇЩњећЬхЬ§аДФмСІЃЌШќКѓЫцЛњГщВщСЫВПЗжбЇЩњЕФГЩМЈЃЈЕУЗжШЁе§ећЪ§ЃЌТњЗжЮЊ100ЗжЃЉНјааЭГМЦЗжЮіЃЌВЂжЦзїГЩЭМБэЃК
зщБ№ | ЗжЪ§ЖЮ | ЦЕЪ§ | ЦЕТЪ |
вЛ | 50.5ЁЋ60.5 | 16 | 0.08 |
Жў | 60.5ЁЋ70.5 | 30 | 0.15 |
Ш§ | 70.5ЁЋ80.5 | m | 0.25 |
ЫФ | 80.5ЁЋ90.5 | 80 | n |
Юх | 90.5ЁЋ100.5 | 24 | 0.12 |
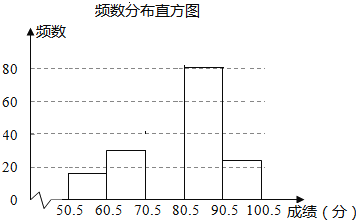
ЧыИљОнвдЩЯЭМБэЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаПЩЬтЃК
ЃЈ1ЃЉетДЮЫцЛњГщВщСЫ______УћбЇЩњЃЌБэжаЕФЪ§m=______ЃЌn=______ЃЛДЫбљБОжаГЩМЈЕФжаЮЛЪ§ТфдкЕк______зщФкЃЛШєЛцжЦЩШаЮЭГМЦЭМЃЌдђдкаожаЁАЕкШ§зщЁБЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ______
ЃЈ2ЃЉВЙШЋЦЕЪ§жБЗНЭМЃЛ
ЃЈ3ЃЉШєГЩМЈГЌЙ§80ЗжЮЊгХауЃЌЧыФуЙРМЦИУаЃАЫФъМЖбЇЩњжаККзжЬ§аДФмСІгХауЕФШЫЪ§ЃЎ