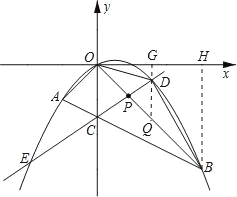
题目内容
【题目】如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n（m＜n）分别是方程x2﹣2x﹣3=0的两根．
（1）求抛物线的解析式；
（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E两点（点D在y轴右侧），连接OD、BD．
①当△OPC为等腰三角形时，求点P的坐标；
②求△BOD 面积的最大值，并写出此时点D的坐标．
【答案】（1）y=
x2+
x；（2）①P点坐标为P1（
，-
）或P2（
，﹣
）或P3（
，﹣
），②D（
，﹣
）．
【解析】试题分析：（1）首先解方程得出A，B两点的坐标，进而利用待定系数法求出二次函数解析式即可；
（2）①首先求出AB的直线解析式，以及BO解析式，再利用等腰三角形的性质得出当OC=OP时，当OP=PC时，点P在线段OC的中垂线上，当OC=PC时分别求出x的值即可；
②利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数，进而得出最值即可．
试题解析：解（1）解方程x2﹣2x﹣3=0，
得 x1=3，x2=﹣1．
∵m＜n，
∴m=﹣1，n=3
∴A（﹣1，﹣1），B（3，﹣3）．
∵抛物线过原点，设抛物线的解析式为y=ax2+bx（a≠0）．
∴
，
解得：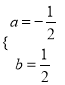 
，
∴抛物线的解析式为y=
x2+
x ．
（2）①设直线AB的解析式为y=kx+b．
∴
；解得：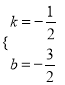 
，
∴直线AB的解析式为y=
x+
．
∴C点坐标为（0，-
）．
∵直线OB过点O（0，0），B（3，﹣3），
∴直线OB的解析式为y=﹣x．
∵△OPC为等腰三角形，
∴OC=OP或OP=PC或OC=PC．
设P（x，﹣x），
（i）当OC=OP时，x2+（-x）2=
．
解得x1=
，x2=-
，（舍去）．
∴P1（
，-
）．
（ii）当OP=PC时，点P在线段OC的中垂线上，
∴P2（
，﹣
）．
（iii）当OC=PC时，由x2+（-x+
）2=
，
解得x1=
，x2=0（舍去）．
∴P3（
，﹣
）．
∴P点坐标为P1（
，-
）或P2（
，﹣
）或P3（
，﹣
）．
②过点D作DG⊥x轴，垂足为G，交OB于Q，过B作BH⊥x轴，垂足为H．
设Q（x，﹣x），D（x，-
x2+
x）．
S△BOD=S△ODQ+S△BDQ=
DQOG+
DQGH，
=
DQ（OG+GH），
=
[x+(
+ 
)]×3，
=-
（x-
）2+
，
∵0＜x＜3，
∴当x=
时，S取得最大值为
，此时D（
，﹣
）．
