题目内容
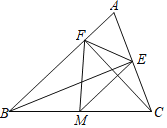
【题目】如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的平分线,求证:
(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.

【答案】(1) 见解析 (2) 见解析
【解析】【试题分析】(1)利用AAS判定证明即可;(2)在平行四边形ABCD中,根据平行四边形的性质得:AD∥BC,根据两直线平行,内错角相等得:∠ADF=∠DEC.
得:∠AFD=∠C.
在△ADF与△DEC中,由三角形内角和定理,∠FAD=∠CDE.得证.
【试题解析】
(1)在△ABE与△AFE中,∠B=∠AFE,∠AEB=∠AEF,AE=AE,∴△ABE≌△AFE(AAS);
(2)平行四边形ABCD中,∵AD∥BC,∴∠ADF=∠DEC.
∵AB∥CD,∴∠C=180°-∠B.
又∠AFD=180°-∠AFE,∠B=∠AFE,
∴∠AFD=∠C.
在△ADF与△DEC中,由三角形内角和定理,得∠FAD=180°-∠ADF-∠AFD,∠CDE=180°-∠DEC-∠C,
∴∠FAD=∠CDE.

练习册系列答案
相关题目