题目内容
14.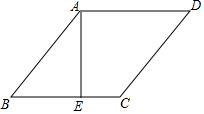 如图,在菱形ABCD中,设AE⊥BC于点E,cosB=$\frac{4}{5}$,EC=2,P为AB上的一个动点,求PE+PC的最小值.
如图,在菱形ABCD中,设AE⊥BC于点E,cosB=$\frac{4}{5}$,EC=2,P为AB上的一个动点,求PE+PC的最小值.
分析 作E关于AB的对称点F,连接CF交AB于P,则CF的长度即为PE+PC的最小值,解直角三角形得到AB=10,BE=8,AE=6,求得EF=2HE=2×$\frac{AE•BE}{AB}$=$\frac{48}{5}$,然后解直角三角形即可得到结论.
解答 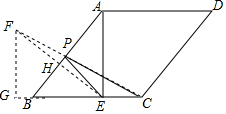 解:作E关于AB的对称点F,连接CF交AB于P,
解:作E关于AB的对称点F,连接CF交AB于P,
则CF的长度即为PE+PC的最小值,
∵cosB=$\frac{4}{5}$,
∴设BE=4a,AB=5a,
∵在菱形ABCD中,AB=BC,
∴5a=4a+2,
∴a=2,
∴AB=10,BE=8,
∴AE=6,
设EF交AB于H,
∴EF=2HE=2×$\frac{AE•BE}{AB}$=$\frac{48}{5}$,
∵∠EFG=∠ABC,
∴FG=EF•$\frac{4}{5}$=$\frac{192}{25}$,GE=EF•$\frac{3}{5}$=$\frac{144}{25}$,
∴CG=$\frac{194}{25}$,
∴CF=$\sqrt{F{G}^{2}+C{G}^{2}}$=10$\sqrt{23}$,
故PE+PC的最小值是10$\sqrt{23}$.
点评 本题考查了菱形的性质、解直角三角形、垂线段最短.解题的关键是求出FE的长.

练习册系列答案
相关题目
3.若$\sqrt{\frac{2y}{3x}}$是二次根式,则x,y应满足条件( )
| A. | y>0,x≥0 | B. | y≥0,x>0 | C. | xy≥0,x≠0 | D. | xy>0 |
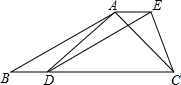 如图,已知四边形ABDE是平行四边形,C为边BD的延长线上一点,连接AC,CE,使AB=AC
如图,已知四边形ABDE是平行四边形,C为边BD的延长线上一点,连接AC,CE,使AB=AC