题目内容
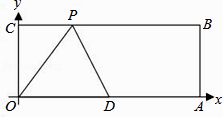
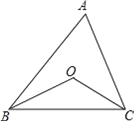
【题目】如图,直角梯形ABCD中,AB//DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C﹣D﹣A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l//AD,与线段CD的交点为E,与折线A﹣C﹣B的交点为Q.点M运动的时间为t(秒).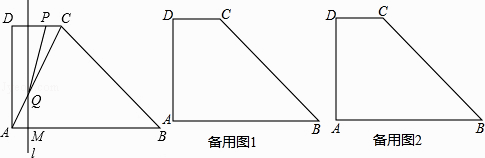
(1)当t=0.5时,求线段QM的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究 ![]() 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.
【答案】
(1)
解:过点C作CF⊥AB于F,则四边形AFCD为矩形.
∴CF=4,AF=2,
此时,Rt△AQM∽Rt△ACF,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴QM=1
(2)
解:∵∠DCA为锐角,故有两种情况:
①当∠CPQ=90°时,点P与点E重合,
此时DE+CP=CD,即t+t=2,∴t=1,在0<t<2内,
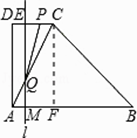
②当∠PQC=90°时,如备用图1,
此时Rt△PEQ∽Rt△QMA,∴ ![]() =
= ![]() ,
,
由(1)知,EQ=EM﹣QM=4﹣2t,
而PE=PC﹣CE=PC﹣(DC﹣DE)=t﹣(2﹣t)=2t﹣2,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,在0<t<2内;
,在0<t<2内;
综上所述,t=1或 ![]()
(3)
解: ![]() 为定值.
为定值.
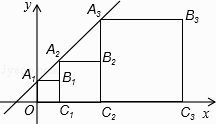
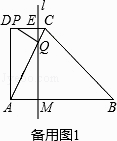
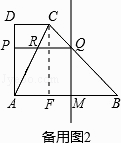
当t>2时,如备用图2,PA=DA﹣DP=4﹣(t﹣2)=6﹣t,
由(1)得,BF=AB﹣AF=4,
∴CF=BF,
∴∠CBF=45°,
∴QM=MB=6﹣t,
∴QM=PA,
∵AB//DC,∠DAB=90°,
∴四边形AMQP为矩形,
∴PQ//AB,
∴△CRQ∽△CAB,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)过点C作CF⊥AB于F,则四边形AFCD为矩形,易知CF=4,AF=2,利用平行线分线段成比例定理的推论可知Rt△AQM∽Rt△ACF,那么可得比例线段,从而求出QM;(2)由于∠DCA为锐角,故有两种情况:
①当∠CPQ=90°时,点P与点E重合,可得DE+CP=CD,从而可求t;②当∠PQC=90°时,如备用图1,容易证出Rt△PEQ∽Rt△QMA,再利用比例线段,结合EQ=EM﹣QM=4﹣2t,可求t;(3) ![]() 为定值.当t>2时,如备用图2,先证明四边形AMQP为矩形,再利用平行线分线段成比例定理的推论可得△CRQ∽△CAB,再利用比例线段可求
为定值.当t>2时,如备用图2,先证明四边形AMQP为矩形,再利用平行线分线段成比例定理的推论可得△CRQ∽△CAB,再利用比例线段可求 ![]() .
.
【考点精析】关于本题考查的相似三角形的应用,需要了解测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能得出正确答案.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】列方程解应用题:五莲县新玛特购物中心第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 20 | 30 |
售价(元/件) | 29 | 40 |
(1)新玛特购物中心将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该购物中心第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?