Question

【题目】如图，抛物线y= x2﹣ x﹣2与x轴交于A、B两点，点P（m，n）（n＜0）为抛物线上一个动点，当∠APB为钝角时，则m的取值范围（ ）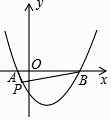
A.﹣1＜m＜0
B.﹣1＜m＜0或3＜m＜4
C.0＜m＜3或m＞4
D.m＜﹣1或0＜m＜3

Answer 1

【答案】B
【解析】解：令y=0得： x2﹣ x﹣2=0， 解得：x=﹣1或x=4，
则点A（﹣1，0）、B（4，0），
以AB为直径作圆M，与y轴交于点P．则抛物线在圆内的部分如图所示，能使∠APB为钝角，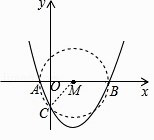

∴M（ ，0），⊙M的半径= ．
在Rt△OMP中，∴OP= =2．
∴P（0，﹣2），
由抛物线的对称性可知，P′（3，﹣2），
∴当﹣1＜m＜0或3＜m＜4时，∠APB为钝角，
故选：B．
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识，掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．