题目内容
如图,在边长为1的正方形网格内,点A、B、C、D、E均在格点处.请你判断∠x+∠y的度数,并加以证明.

答:∠x+∠y=45°. ……………………………………1分
证明:如图,以AG所在直线为对称轴,作AC的轴对称图 形AF,连结BF,

∵网格中的小正方形边长为1,且A、B、F均在格点处,
∴AB=BF= ,AF=
,AF= .
.
∴
∴△ABF为等腰直角三角形,且∠ ABF=90°. …………………2分
ABF=90°. …………………2分
∴∠BAF=∠BFA=45°.
∵AF与AC关于直线AG轴对称,
∴∠FAG=∠CAG.
又∵AG∥EC,
∴∠x=∠CAG.
∴∠x=∠FAG. ………………………………………………………3分
∵DB∥AG,
∴∠y=∠BAG. ………………………………………………………4分
∴∠x+∠y=∠FAG+∠BAG =45°. ………………………………5分
证明:如图,以AG所在直线为对称轴,作AC的轴对称图 形AF,连结BF,

∵网格中的小正方形边长为1,且A、B、F均在格点处,
∴AB=BF=
 ,AF=
,AF= .
.∴

∴△ABF为等腰直角三角形,且∠
 ABF=90°. …………………2分
ABF=90°. …………………2分∴∠BAF=∠BFA=45°.
∵AF与AC关于直线AG轴对称,
∴∠FAG=∠CAG.
又∵AG∥EC,
∴∠x=∠CAG.
∴∠x=∠FAG. ………………………………………………………3分
∵DB∥AG,
∴∠y=∠BAG. ………………………………………………………4分
∴∠x+∠y=∠FAG+∠BAG =45°. ………………………………5分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
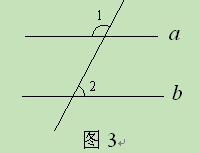
 =20°,则
=20°,则
 ,∠1=60°,∠2=50°,则
,∠1=60°,∠2=50°,则 ( )
( )