ĢāÄæÄŚČŻ
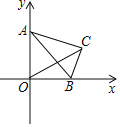
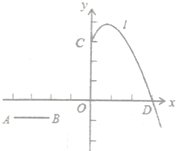
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćOĪŖ×ų±źŌµć£¬Ö±Ļßy£½©x+b½»yÖįÓŚµćA£¬½»xÖįÓŚµćB£¬S”÷AOB£½![]() £®
£®
£Ø1£©ĒóbµÄÖµ£»
£Ø2£©µćCŅŌĆæĆė1øöµ„Ī»³¤¶ČµÄĖŁ¶Č“ÓOµć³ö·¢ŃŲxÖįĻņµćBŌĖ¶Æ£¬µćDŅŌĆæĆė2øöµ„Ī»³¤¶ČµÄĖŁ¶Č“ÓAµć³ö·¢ŃŲyÖįĻņµćOŌĖ¶Æ£¬C£¬DĮ½µćĶ¬Ź±³ö·¢£¬µ±µćDŌĖ¶Æµ½µćOŹ±£¬C£¬DĮ½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®Į¬½ÓCD£¬ÉčµćCµÄŌĖ¶ÆŹ±¼äĪŖtĆė£¬”÷CDOµÄĆ껿ĪŖS£¬ĒóSÓėtµÄŗÆŹż¹ŲĻµŹ½£Ø²»ŅŖĒ󊓳ö×Ō±äĮætµÄȔֵ·¶Ī§£©£»
£Ø3£©ŌŚ£Ø2£©Ģõ¼žĻĀ£¬¹żµćC×÷CE”ĶCD½»ABÓŚµćE£¬¹żµćD×÷DF”ĪxÖį½»ABÓŚµćF£¬¹żµćF×÷FH”ĶCE£¬“¹×ćĪŖH£®ŌŚCHÉĻČ”µćM£¬Ź¹µĆMH£ŗHE£½8£ŗ33£¬Į¬½ÓFM£¬Čō”ĻFMH£½![]() ”ĻFEH£¬ĒótµÄÖµ£®
”ĻFEH£¬ĒótµÄÖµ£®
”¾“š°ø”æ£Ø1£©b£½9£»£Ø2£©S£½©t2+![]() £»£Ø3£©t£½1
£»£Ø3£©t£½1
”¾½āĪö”æ
£Ø1£©ÓÉÖ±Ļß½āĪöŹ½æɵĆA”¢BĮ½µć×ų±ź£¬øł¾Ż”÷AOBµÄĆ껿ĮŠ·½³Ģ½ā³öbµÄÖµ£®
£Ø2£©·Ö±šÓĆt±ķŹ¾OCŗĶODµÄ³¤¼“æɵƵ½SÓėtµÄ±ķ“ļŹ½£®
£Ø3£©Ź×ĻČøł¾ŻĢāŅā»³öŹ¾ŅāĶ¼£¬Č»ŗóøł¾ŻĖłøų¶ØµÄĻ߶ĪµČĮæ¹ŲĻµÓė½Ē¶ČµČĮæ¹ŲĻµĶʵ¼³ö”ĻFEMµÄÕżĒŠÖµ£¬¹żµćE×÷GP”ĶOBÓŚP½»DFµÄŃÓ³¤ĻßÓŚµćG£¬æÉŅŌĶĘÖ¤”ĻDEG£½”ĻFEM£¬ÓŚŹĒĄūÓĆ”ĻDEGµÄÕżĒŠÖµĮŠ³ö±ČĄż·½³Ģ£¬×īŗó½ā³ötµÄÖµ£®
½ā£ŗ£Ø1£©ČēĶ¼1£¬
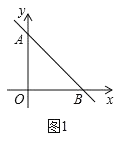
”ßÖ±Ļßy£½©x+b½»yÖįÓŚµćA£¬½»xÖįÓŚµćB£¬
”ąA£Ø0£¬b£©£¬B£Øb£¬0£©
”ąOA£½OB£½b£¬
”ąS”÷AOB£½![]() £½
£½![]() £®
£®
”ąb£½9»ņ-9£Ø²»·ūŗĻÓėyÖįµÄ½»µć£¬ÉįČ„øŗÖµ£©£®
£Ø2£©ČēĶ¼2£¬
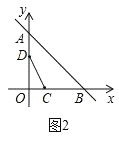
ÓÉĢāŅāÖŖOC£½t£¬AD£½2t£¬ŌņOD£½OA©AD£½9©2t£¬
”ąS£½![]() ODOC£½
ODOC£½![]() t£Ø9©2t£©£½©t2+
t£Ø9©2t£©£½©t2+![]() £®
£®
£Ø3£©”ß![]() £½
£½![]() £¬
£¬
”ąÉčMH£½8k£¬HE£½33k£¬
ČēĶ¼3£¬ŌŚHEÉĻ½ŲČ”HN£½MH£½8k£¬Į¬½ÓFN£¬
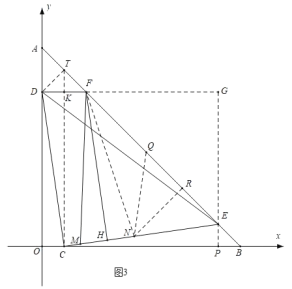
ŌņEN£½EH©HN£½25k£¬
”ßFH”ĶCEÓŚH£¬
”ąFM£½FN£¬”ĻFME£½”ĻFNM£¬
”ß”ĻFME£½![]() ”ĻFEM£¬
”ĻFEM£¬
”ąÉč”ĻFEM£½2¦Į£¬”ĻFME£½3¦Į£¬
”ą”ĻFNM£½3¦Į£¬
”ß”ĻFNM£½”ĻNFE+”ĻFEN£¬
”ą”ĻNFE£½”ĻFNM©”ĻFEM£½3¦Į©2¦Į£½¦Į£¬
ŌŚFEÉĻČ”Ņ»µćQ£¬Į¬½ÓNQ£¬Ź¹NQ£½NE£½25k£¬
Ōņ”ĻNQE£½”ĻFEM£½2¦Į£¬
”ß”ĻNQE£½”ĻNFE+”ĻQNF£½¦Į+”ĻQNF£¬
”ą”ĻNF£½¦Į£½”ĻNFE£¬
”ąFQ£½NQ£½25k£¬
×÷NR”ĶQEÓŚR£¬ŌņQR£½RE£½n£¬
”ąFE£½FQ+QE£½25k+2n£¬
”ßcos”ĻFEH£½cos2¦Į£½![]() £½
£½![]() £¬
£¬
”ą![]() £½
£½![]() £¬
£¬
½āµĆn£½15k£¬
”ąQR£½RE£½15k£¬
”ąNR£½![]() £½20k£¬
£½20k£¬
”ątan2¦Į£½![]() £½
£½![]() £®
£®
¹żµćE×÷GP”ĶOBÓŚP½»DFµÄŃÓ³¤ĻßÓŚµćG£¬
”ą”ĻCPE£½”ĻBPE£½90”ć£¬
”ßOA£½OB£½9£¬
”ą”ĻOAB£½”ĻOBA£½45”ć£¬
”ą”ĻPEB£½45”ć£¬
”ąBP£½PE£¬
”ßDF”ĪOB£¬
”ą”ĻODF£½”ĻADF£½90”ć£¬
”ąĖıߊĪDOPGĪŖ¾ŲŠĪ£¬
”ąGP£½OD£¬DG£½OP£¬
×÷CT”ĶOB½»ABÓŚT£¬½»DFÓŚK£¬Į¬½ÓDT£¬
ŌņODKCĪŖ¾ŲŠĪ£¬”÷CTBĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąDK£½OC£½t£¬CK£½OD£¬CT£½CB£¬
”ß”ĻFDA£½90”ć£¬”ĻFAF£½45”ć£¬
”ą”÷ADFĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąDF£½AD£½2OC£½2t£¬
”ąKĪŖDFÖŠµć£¬
”ąTĪŖAFÖŠµć£¬
”ą”÷DTFĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻDTK£½”ĻFTK£½45”ć£¬
”ßDC”ĶCE£¬
”ą”ĻDCT+”ĻTCE£½”ĻTCE+”ĻBCE£½90”ć£¬
”ą”ĻDCT£½”ĻECB£¬
ŌŚ”÷DCTŗĶ”÷ECBÖŠ£ŗ
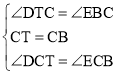
”ą”÷DCT”Õ”÷ECB£ØASA£©£¬
”ąCD£½CE£¬
”ą”÷DCEĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻCED£½45”ć£¬
”ß”ĻDCO+”ĻECP£½”ĻDCO+”ĻODC£½90”ć£¬
”ą”ĻODC£½”ĻECP£¬
ŌŚ”÷DOCŗĶ”÷CPEÖŠ£ŗ
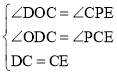
”ą”÷DOC”Õ”÷CPE£ØAAS£©£¬
”ąBP£½PE£½OC£½t£¬
”ąDG£½OP£½OB©PB£½9©t£¬
”ąFG£½DG©DF£½9©3t£¬
”ß”ĻGFE£½”ĻAFD£½45”ć£¬”ĻGEF£½”ĻBEP£½45”ć£¬
”ąDE£½GF£½9©3t£¬
”ß”ĻDEG£½”ĻFEG+”ĻFED£½45”ć+”ĻFED£½”ĻDEC+”ĻFED£½”ĻFEM£½2¦Į£¬
”ątan”ĻDEG£½![]() £½
£½![]() £½
£½![]() £¬
£¬
½āµĆt£½1£®

 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø