Question

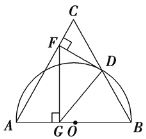
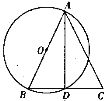
【题目】如图，在△ABC中，以AB为直径的⊙O交BC于点D，连结AD，请你添加一个条件，使△ABD≌△ACD，并说明全等的理由．

你添加的条件是

Answer 1

【答案】AB＝AC或BD＝DC等，详见解析

【解析】

因为AB是⊙O的直径，所以∠ADB=∠ADC=90°，即AD是BC边上的高，可添加AB=AC，当AB=AC时，△ABC是等腰三角形，由等腰三角形的性质可知，∠ABD=∠ACD及底边上的高与底边上的中线重合，即BD=CD，可根据“SSS”，“H.L”，“SAS”，“AAS”，“ASA”证明△ABD≌△ACD.

解：本题答案不唯一，添加的条件可以是

①AB＝AC，②∠B＝∠C，③BD＝DC（或D是BC中点），

④∠BAD＝∠CAD（或AD平分∠BAC）等．

添加的条件是AB＝AC

理由如下：

∵AB是⊙O的直径

∴∠ADB=∠ADC=90°

在Rt△ABD和Rt△ACD中，

∴Rt△ABD≌Rt△ACD(H.L)

即△ABD≌△ACD.