Question

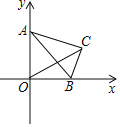
【题目】如图，点在直线上，过点作，且，点在射线上（点不与点重合），且满足，，与交于点，过点作于点．设．

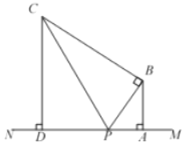
（1）用含的代数式表示的长；

（2）①线段的长是________；

②线段的长是_________；（用含的代数式表示）

（3）当为何值时，有最小值？并求出这个最小值．

Answer 1

【答案】（1）；（2）①；②；（3）时，的最小值．

【解析】

（1）首先证明，然后根据相似三角形性质进一步得出，再结合勾股定理所得的进一步对式子进行分析求解即可；

（2）①延长和交于点，通过证明，由此进一步得出，然后再证明出，最后利用相似三角形性质求出CD即可；②先证明，据此进一步得出，由此得出，最后进一步证明，从而得出答案即可；

（3）过点作于点，通过证明，由此得出，然后得出，根据当点运动时，总有，所以当点与点重合，即时，的最小值，由此求出的最小值，最后根据题意进一步求出即可.

（1）在和中，

∵，90°，

∴，

∴，即，

又根据勾股定理可得：，

∴，

∴；

（2）

①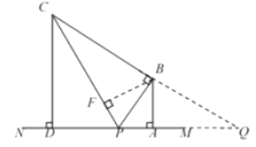

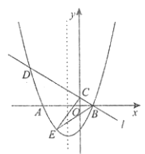
如图，延长和交于点，

∵，，且，

∴，则有，即，

又∵，

∴，

∴，

∵，

∴；

②∵，，

∴∠ABP+∠APB=∠ABP+∠ABQ=90°，

∴∠APB=∠ABQ，

∴，

∴，

∴，

即，

∴，

由①知，结合可得：，

∴，

∴，

故答案为：①8；②；

（3）

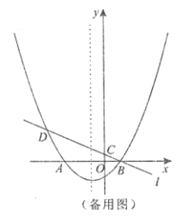
如图，过点作于点，

∵∠BAP=∠BFP，∠APB=∠FPB，PB=PB，

∴，

∴，

∴，

又∵，

∴当点运动时，总有，

∴当点与点重合，即时，的最小值，

则的最小值．

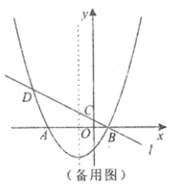
此时，如图所示，

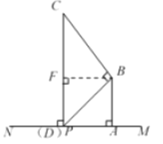
其中，即，解得或（不符合题意，舍去）．