题目内容
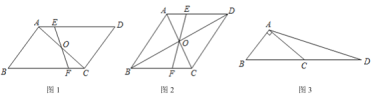
【题目】(1)如图 1,在平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,过点
的中点,过点![]() 的直线分别交
的直线分别交![]() 于点
于点![]() 若平行四边形
若平行四边形![]() 的面积是 8,则四边形
的面积是 8,则四边形![]() 的面积是___________ .
的面积是___________ .
(2)如图 2,在菱形![]() 中,对角线相交于点 O,过点 O 的直线分别交
中,对角线相交于点 O,过点 O 的直线分别交![]() 于点
于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 的面积.
的面积.
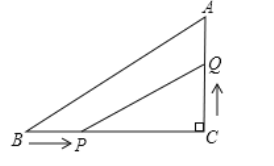
(3)如图 3,在![]() 中,
中,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,若
,若![]() ,则
,则![]() 的面积是____________ .
的面积是____________ .
【答案】(1)4;(2)![]() ;(3)3
;(3)3
【解析】
(1)首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS定理证明△AEO≌△CFO,再根据全等三角形的性质可得结论;
(2)根据菱形的性质得到AD∥BC,AO=CO=![]() AC=2.5,BO=
AC=2.5,BO=![]() BD=5,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
BD=5,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;
(3)延长AC到E使CE=AC=3,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到 ![]() ,即可得到结论.
,即可得到结论.
(1)∵四边形![]() 是平行四边形,
是平行四边形,
![]()
![]()
在△AOE 和△COF 中
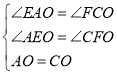
![]()
![]()
(2)∵四边形![]() 是菱形,
是菱形,
![]()
![]()
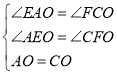
![]()
![]()
![]()
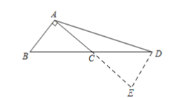
(3)如图,延长![]() 到 E 使
到 E 使![]() ,连结 DE,
,连结 DE,
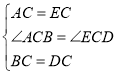
![]()
![]() ,
,
∵![]() ,
,
∴![]()
∴![]()
![]() .
.

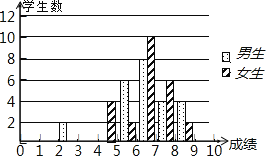
【题目】为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
男生 | 6.9 | 2.4 | ______ | 91.7% | 16.7% |
女生 | ______ | 1.3 | ______ | 83.3% | 8.3% |
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?