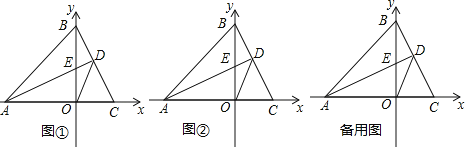
题目内容
【题目】如图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE.求证:BD=2CE.
【答案】见解析.
【解析】
延长CE、BA交于F点,然后证明△BFC是等腰三角形,再根据等腰三角形的性质可得CE=![]() CF,然后在证明△ADB≌△AFC可得BD=FC,进而证出BD=2CE.
CF,然后在证明△ADB≌△AFC可得BD=FC,进而证出BD=2CE.
延长CE、BA交于F点,如图,
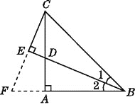
∵BE⊥EC,
∴∠BEF=∠CEB=90°.
∵BD平分∠ABC,
∴∠1=∠2,
∴∠F=∠BCF,
∴BF=BC,
∵BE⊥CF,
∴CE=![]() CF,
CF,
∵△ABC中,AC=AB,∠A=90°,
∴∠CBA=45°,
∴∠F=(180-45)°÷2=67.5°,∠FBE=22.5°,
∴∠ADB=67.5°,
∵在△ADB和△AFC中,
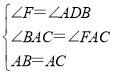 ,
,
∴△ADB≌△AFC(AAS),
∴BD=FC,
∴BD=2CE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目