题目内容
【题目】在平面直角坐标系中,o为坐标原点,点A的坐标为(![]() ,3),点B的坐标(
,3),点B的坐标(![]() ,6).
,6).
(1)若AB与坐标轴平行,求AB的长;
(2)若![]() 满足
满足![]() AC⊥
AC⊥![]() 轴,垂足为C,BD⊥
轴,垂足为C,BD⊥![]() 轴,垂足为D:
轴,垂足为D:
①求四边形ACDB的面积;
②连AB、OA、OB,若△OAB的面积大于6而小于10,求![]() 的取值范围。
的取值范围。
【答案】(1)AB=3;(2)①9;②6<a<![]() 或﹣
或﹣![]() <a<﹣2
<a<﹣2
【解析】
(1)分析题意可知,AB与y轴平行,则AB的长为两点的纵坐标之差;
(2)①先解方程组得到b﹣a=2,则根据梯形的面积公式可计算出四边形ACDB的面积为9;
②分类讨论:当a>0,S△OAB=S△OBD﹣S△OAC﹣S梯形ACDB=![]() a﹣3,则6<
a﹣3,则6<![]() a﹣3<10,解得6<a<
a﹣3<10,解得6<a<![]() ;当a<0,b>0,S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=3﹣
;当a<0,b>0,S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=3﹣![]() a,则6<3﹣
a,则6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,而b=2+a>0,则a>﹣2,故舍去;当a<0,b<0,S△OAB=S△OBD+S梯形ACDB﹣S△OAC=3﹣
<a<﹣2,而b=2+a>0,则a>﹣2,故舍去;当a<0,b<0,S△OAB=S△OBD+S梯形ACDB﹣S△OAC=3﹣![]() a,则6<3﹣
a,则6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,于是得到a的取值范围为6<a<
<a<﹣2,于是得到a的取值范围为6<a<![]() 或﹣
或﹣![]() <a<﹣2.
<a<﹣2.
(1)∵AB与坐标轴平行,即AB平行于y轴,
∴AB=6﹣3=3;
(2)①由方程组![]() 得b﹣a=2,
得b﹣a=2,
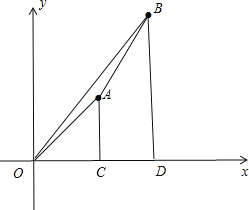
∵AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,
∴C(a,0),D(b,0),如图,
∴四边形ACDB的面积=![]() (3+6)(b﹣a)=
(3+6)(b﹣a)=![]() 92=9;
92=9;
②当a>0,
∵S△OAB=S△OBD﹣S△OAC﹣S梯形ACDB,
∴S△OAB=![]() 6b﹣
6b﹣![]() 3a﹣9=3b﹣
3a﹣9=3b﹣![]() a﹣9,
a﹣9,
而b=2+a,
∴S△OAB=3(2+a)﹣![]() a﹣9=
a﹣9=![]() a﹣3,
a﹣3,
∴6<![]() a﹣3<10,解得6<a<
a﹣3<10,解得6<a<![]() ;
;
当a<0,b>0,
S△OAB=S梯形ACDB﹣S△OBD﹣S△OAC=9﹣![]() 6b+
6b+![]() 3a=9﹣3b+
3a=9﹣3b+![]() a=9﹣3(2+a)+
a=9﹣3(2+a)+![]() a=3﹣
a=3﹣![]() a
a
∴6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,
<a<﹣2,
而b=2+a>0,则a>﹣2,故舍去,
当a<0,b<0,
∵S△OAB=S△OBD+S梯形ACDB﹣S△OAC=﹣![]() 6b+9+
6b+9+![]() 3a=﹣3b+9+
3a=﹣3b+9+![]() a=﹣3(2+a)+9+
a=﹣3(2+a)+9+![]() a=3﹣
a=3﹣![]() a
a
∴6<3﹣![]() a<10,解得﹣
a<10,解得﹣![]() <a<﹣2,
<a<﹣2,
综上所述,a的取值范围为6<a<![]() 或﹣
或﹣![]() <a<﹣2.
<a<﹣2.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀. 为了解本次大赛的成绩,校团委随机抽取了甲、乙两组学生成绩作为样本进行统计,绘制了如下统计图表:
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.8 | a | 3.76 | 90% | 30% |
乙组 | b | 7.5 | 1.96 | 80% | 20% |
(1)求出表中a,b的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面的表格判断,小英属于哪个组?
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组. 但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.